= vd - vdr - R x1 + N L (W iq - W r iqr)
- TS Electrotechnique
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes
glissants - Conversion sigma-delta - Modulation AM - Commande avec
frottement sec
Approche de l’automatique non linéaire par les méthodes de Lyapunov
III Commande utilisant une fonction de Lyapunov
La recherche d’une loi de commande garantissant la stabilité d’un système asservi peut se faire à l’aide des fonctions de Lyapunov (seconde méthode) : si la loi de commande garantit la négativité de la dérivée dV/dt d’une fonction positive V(x), alors le système ainsi commandé sera stable.
III.1 L’exemple choisi : moteur pas à pas
On traite ici l’exemple d’un moteur pas à pas à aimant permanent (semblable à une machine synchrone à aimant permanent) et nous cherchons une loi de commande garantissant la convergence asymptotique de l’écart de trajectoire vers 0. Pour alléger la démarche, on considère seulement la commande en vitesse, dans le repère tournant du rotor :
L = vd - vdr - R x1 + N L (W iq - W r iqr)
L 
= vq - vqr - R x2
- N L (W id - W r
idr) - K x3
J 
= K x2 - fv
x3
avec comme vecteur d’état : e = [ x1 x2 x3 ]T = [ id-idr iq-iqr W - W r ]T et :
id courant direct au stator, idr le courant de référence à suivre
iq courant d’axe en quadrature, iqr sa référence
vd , vdr , vq ,vqr : les tensions statoriques définies de la même manière
W vitesse angulaire , W r sa référence
R , L résistance et inductance au stator
J ,
fv moment d’inertie et coefficient de frottement visqueuxK constante de fcem , ou constante de couple
N nombre de dents au rotor ( le nombre de pas par tour est 4 N)
III.2 Fonction de Lyapunov
Choisissons par exemple la fonction de Lyapunov :
V(e) = 1/2 eT.A. e = 1/2 (L x1² +L x2² +J x3²) ; A = diag( L,L,J)
qui est globalement définie positive, et s’annule seulement à l’origine. La dérivée de V par rapport au temps le long des trajectoires du système est donnée par :
(e) = L x1 
+ L x2 
+ J x3 
En utilisant le fait que : W id - W r idr = x1 x3 + W r x1 + x3 idr
W iq - W r iqr = x2 x3 + W r x2 + x3 iqr
cette dérivée s’écrit :
(e) = - R (x1² + x2²) -fv
x32 - x2 x3 NL idr + x1
x3 NL iqr + x1 (vd - vdr) + x2
(vq - vqr)
III.3 Loi de commande par retour d’état pour le moteur pas à pas
On désire que (e) soit définie négative, et s’annule à
l’origine. Nous allons donc chercher à garantir :
x1 (vd - vdr) + x2 (vq - vqr)- x2 x3 NL idr + x1 x3 NL iqr £ R (x1² + x2²) + fv x32
Il est souhaitable de s’affranchir des termes liés à la référence. La commande peut alors être choisie de sorte à compenser ces termes et introduire le retour d’état vd’(e) , vq’(e) :
vd = vdr - N L x3 iqr + vd’(e)
vq = vqr + N L x3 idr + vq’(e)
Une forme très générale pour v’d et v’q est celle d’un retour d’état linéaire :
v’d = l 1 x1 + l 2 x2 +l 3 x3
v’q = m 1 x1 + m 2 x2+ m 3 x3
pour lequel nous devons donc garantir, afin d’avoir (e) £ 0 :
x1 v’d + x2 v’q - R (x1² + x2²) - fv x3² £ 0
Il vient alors la condition :
l 1 x12 + l 2 x1 x2 +l 3 x1 x3 + m 1 x1 x2 + m 2 x22 + m 3 x2 x3 £ R (x1² + x2²) + fv x3²
qui peut s’écrire (e) = - eT P e , avec P
définie positive.
Un choix simple consiste à poser l 1 = l 2 = m 1 = m 2 = 0 ; l 3 = l ; m 3 = m qui conduit à la loi de commande :
vd = vdr + (- N L iqr + l ) x3
vq = vqr + (N L idr + m ) x3
et la matrice P devient alors :
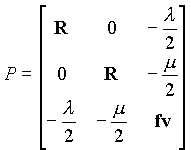
dont les valeurs propres sont :
p1 = R ; p2,3 = 1 { R + fv ! [ (R - fv)2 + l 2 + m 2] 1 }
qui sont toutes trois positives pour
l 2 + m 2 < 4 fv R
III.4 Discussion sur la commande du moteur pas à pas
Cette loi de commande, valable pour l et m nuls, présente l’intérêt de ne pas nécessiter de mesure des courants - la dynamique de ceux-ci est fixée par les propriétés naturelles du circuit électrique de la machine - . Comme cette commande ne contrôle que la vitesse, il est évidemment nécessaire d’introduire un retour sur la position de manière à éviter les dérives. On peut envisager d’implanter en amont un correcteur de position PID par exemple.
(Vous pouvez voir aussi une étude de la commande de cette machine par les modes glissants.)
Page suivante |
- TS Electrotechnique
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes
glissants - Conversion sigma-delta - Modulation AM - Commande avec
frottement sec