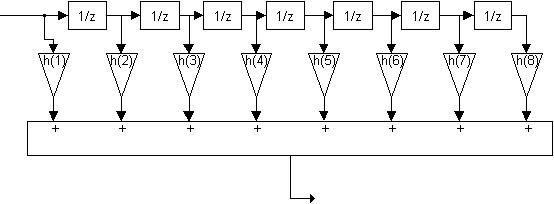
Filtre à Réponse Impulsionnelle Finie (RIF)
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec
Filtre à Réponse Impulsionnelle Finie (RIF)
Les filtres de ce type ont pour fonction de transfert
en Z : 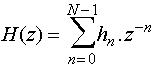
On sait d'autre part que l'on peut doter ces filtres d'une fonction de transfert à déphasage linéaire en imposant que les coefficients hn présentent une symétrie (paire ou impaire).
Dans ce qui suit, on s'intéresse à l'élaboration de filtres RIF passe-bas par la méthode dite de "l'échantillonnage de la réponse impulsionnelle". Pour que le problème présente un intérêt, on s'imposera que la plus haute fréquence de coupure ne soit pas trop grande par rapport à la fréquence d'échantillonnage fech . On s'astreindra en outre à ce que le filtre comporte un nombre N d'étages raisonnablement petit.
Données du problème :
fech = 1000 Hz ; fc = 250 Hz ; N = 8
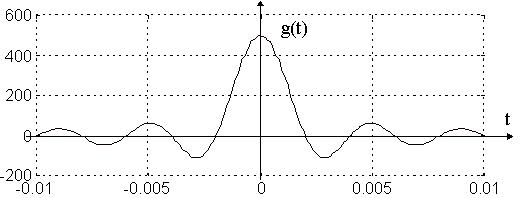
a) On calcule la réponse impulsionnelle g(t) d'un filtre passe-bas idéal fc :
![]()
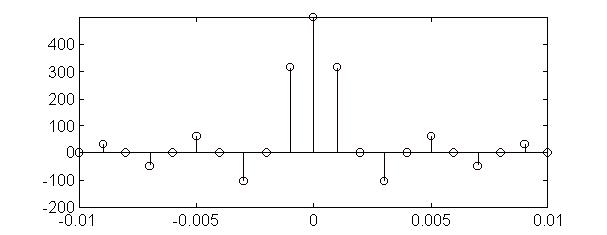
b) On échantillonne cette réponse à la cadence Tech = 1/ fech :
c) On conserve N échantillons, par exemple à t = 0 ... 7 . Tech
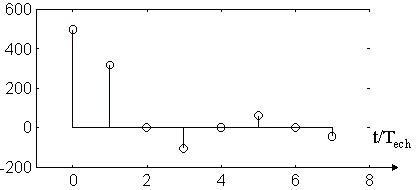
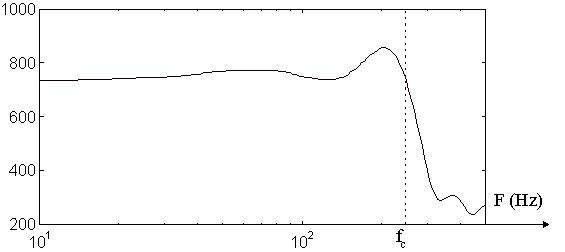
Ces échantillons ont pour valeur :
| n = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| hn = 500 | 318.31 | 0.0025 | -106.10 | -0.0013 | 63.66 | 0.0008 | -45.47 |
d) On peut calculer la réponse fréquentielle (transmittance isochrone) donnée par :
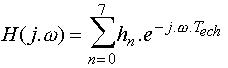
dont le module est représenté ci-dessous en fonction de la fréquence du signal incident :
Cette réponse en fréquence est périodique, de période fech , et présente une symétrie paire puisque le signal impulsionnel est réel ; aussi n'a-t-on représenté la transmittance isochrone que jusqu'à fech / 2 , soit 500 Hz. On peut noter que la réponse est fortement ondulée. On va tâcher de remédier à ce fait en augmentant le nombre d'échantillons : N = 15. (Fech et fc restent inchangés).
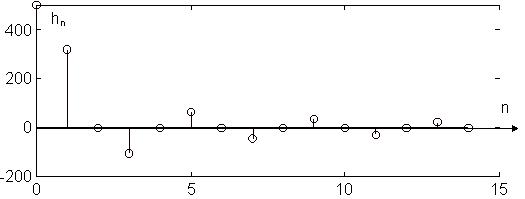
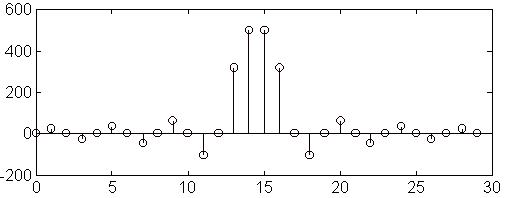
La même procédure donne les échantillons suivants :
| 500 | 318.31 | 0.0025 | -106.10 | -0.0013 | 63.66 | 0.0008 | -45.47 |
| -0.0006 | 35.37 | 0.0005 | -28.94 | -0.0004 | 24.45 | 0.0004 |
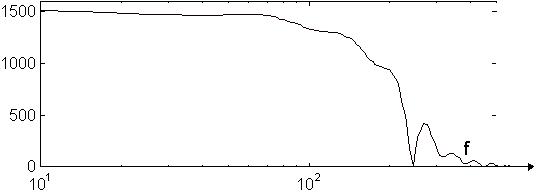
La réponse fréquentielle est alors la suivante :
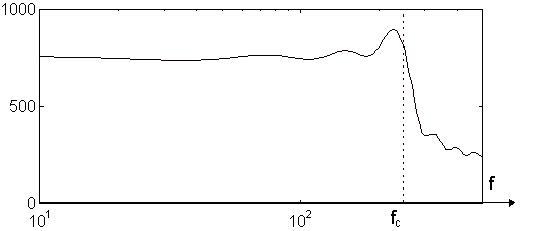
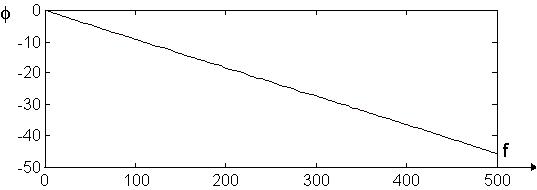
On constate que la situation ne s'est pas améliorée pour ce qui concerne le rapport d'amplitude des résonnances ; le phénomène de Gibbs lié à la troncature de la réponse impulsionnelle n'a été que rendu plus "serré", il ne dépend pas du nombre d'échantillons. Quant à la réponse de phase, elle présente l'allure suivante :
On peut souhaiter conserver le caractère passe-bas du filtre tout en cherchant à obtenir une phase linéaire ; rendons symétrique la réponse impulsionnelle précédemment utilisée :
On obtient les réponses suivantes en module et en phase (avec un filtre qui comporte à présent 30 étages) :
On obtient bien un filtre à phase linéaire, ainsi qu'il est prévu.
On représente ci-dessous le dispositif employé pour réaliser le filtre d'ordre 8 :
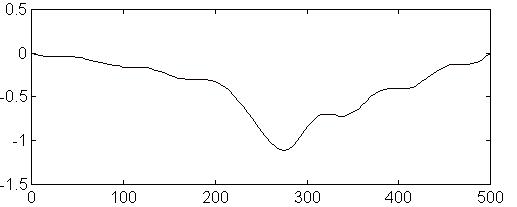
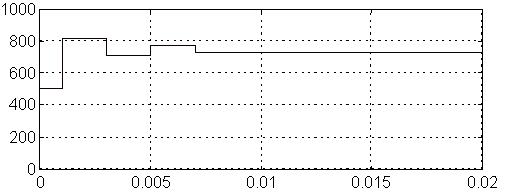
Réponses indicielles des filtres précédents
Réponse indicielle du filtre d'ordre 8
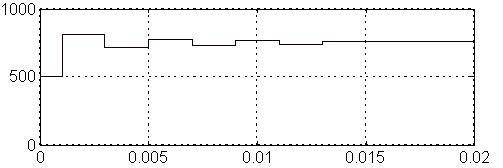
Réponse indicielle du filtre d'ordre 15
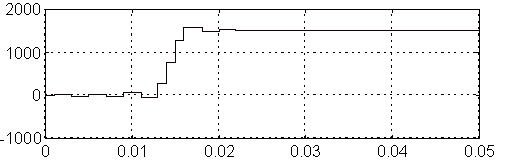
Réponse indicielle du filtre d'ordre 30 à coefficiets symétriques
La distorsion de la réponse en fréquence dûe au phénomène de Gibbs peut être atténuée en tronquant la réponse impulsionnelle, non pas par une fenêtre rectangulaire, mais par une fenêtre d'adoucissement. (L'étude des fonctions fenêtres peut être trouvée dans les ouvrages sur les filtres ou l'analyse spectrale.)
La détermination formelle de la réponse impulsionnelle d'un filtre peut cependant poser des problèmes lorsque l'atténuation du filtre est complexe. On emploie alors d'autres méthodes, parmi lesquelles l'une des plus simples consiste à échantillonner la réponse fréquentielle, puis à calculer la réponse impulsionnelle par un algorithme de transformation de Fourier inverse.
Script matlab
Définitions des grandeurs
fc=250;,fe=1000;,T=1/fe;
sinus cardinal échantillonné à fe
t=-0.02000001:T:0.02;,g=2*fc*sin(2*pi*fc*t)./(2*pi*fc*t);,stem(t,g)
axis([-0.01001 0.01 -200 500])
Troncature à 8 échantillons
h=g(11:18);
t=0:7;
stem(t,h), axis([-1 8 -200 600])
Réponse fréquentielle
f=logspace(1,3,200);
p=-2*pi*f*T*j;
PP=[0:7]'*p; % somme des h(n)*exp(-2*j*pi*f*T*n)
PP=exp(PP);
H=h*PP;
semilogx(f,abs(H))
hold on,line([250 250],[200 1000])
Fin
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec