- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec
Etude d'un Système Dynamique avec Frottement Sec
Soit le système non-linéaire suivant :
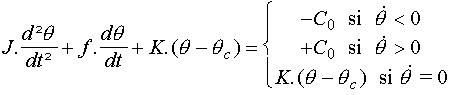
Le comportement de ce système est décrit
par trois systèmes linéaires ; étudions tout d'abord
ce comportement pour ![]() :
:
Le système possède alors un point d'équilibre 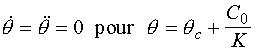 . Déplaçons l'équilibre en posant le changement de
variable :
. Déplaçons l'équilibre en posant le changement de
variable :
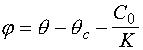
L'équation s'écrit dans le nouvel espace d'état :
![]()
qui possède un point d'équilibre en ![]() .
.
Ecrivons cette équation différentielle sous forme d'état :
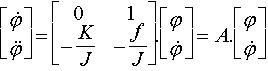
et représentons-la dans la base des vecteurs propres de la matrice d'état A, dont les valeurs propres sont :
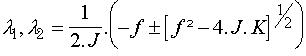
Afin de ne pas alourdir cette présentation, effectuons dès à présent une application numérique :
f=55.10-3N.m / rad.s-1 , J=20.10-3 kg.m² et K=0,1 (valeurs choisies pour avoir une réponse pseudo-oscillante). On a dans ce cas :
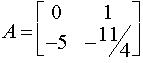 de valeurs propres :
de valeurs propres : 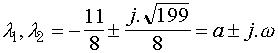
Soit la matrice : 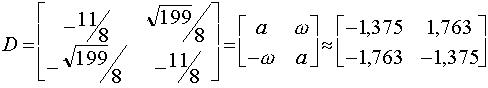
Le système différentiel : 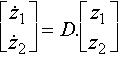
est obtenu à partir du système différentiel
: 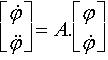
par le changement de variable ( changement de base ) :
z = V . j ; A = V . D . V-1 avec
: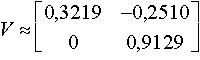
(matrice réelle de vecteurs propres).
Il est très intéressant d'étudier la réponse du système :
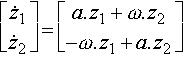
sous sa forme polaire en posant :
z1 = r.cosq
z2 = r.sinq
On a :
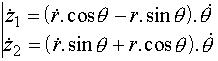
et aussi :
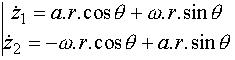
En partant par exemple de : r² = z1² + z2² et en dérivant, on a :
![]()
d'où l'on tire :
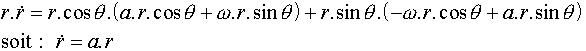
De même, on peut écrire :
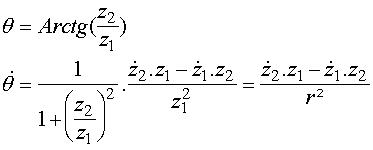
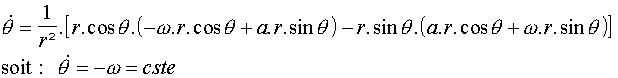
Par conséquent, pour un état initial : 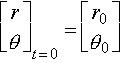 , le système évolue selon l'équation :
, le système évolue selon l'équation :
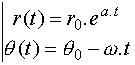
L'équation d'état du système représenté sous forme polaire dans l'espace d'état {z1 , z2}est :
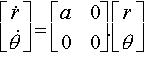
Elle définit un système parfaitement découplé : l'évolution de r(t) est indépendante de celle de q(t).
La trajectoire dans le plan (z1 , z2 ) est ainsi une spirale logarithmique. Si a = 0 , les trajectoires sont des cercles dont le centre est l'origine.
Dans l'espace d'état initial ![]() , les trajectoires sont les transformées des trajectoires dans le
plan (z1 , z2 ) par
:
, les trajectoires sont les transformées des trajectoires dans le
plan (z1 , z2 ) par
:
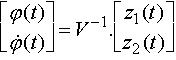
Or, dans le plan (z1 ,
z2 ), un cercle centré sur l'origine
a pour équation : ![]()
qu'on peut aussi écrire sous forme quadratique :
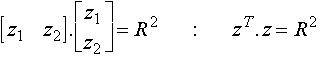
Dans le repère initial ![]() ,
les cercles sont transformés en :
,
les cercles sont transformés en :
(V-1.z)T.(V-1. z) = R²
soit encore :
zT.(V-1 T.V-1). z = R²
On montre dans les ouvrages d'algèbre linéaire appliquée à la géométrie que les axes de cette ellipse sont les directions propres de la matrice symétrique (V.VT)-1 .La direction propre associée à la plus grande valeur propre est celle du petit axe (resp. : la plus petite valeur propre : le grand axe). [La longueur d'un axe est l'inverse de la racine carrée de la valeur propre associée.]
(N.B.: si l'une des valeurs propres est nulle, le problème est compliqué : l'un des axes est infini.)
Dans notre cas, on a :
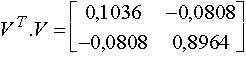
| valeur propre | vecteur propre |
| 0,0955 | 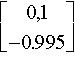 grand axe
grand axe |
| 0,9045 | 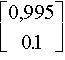 petit axe
petit axe |
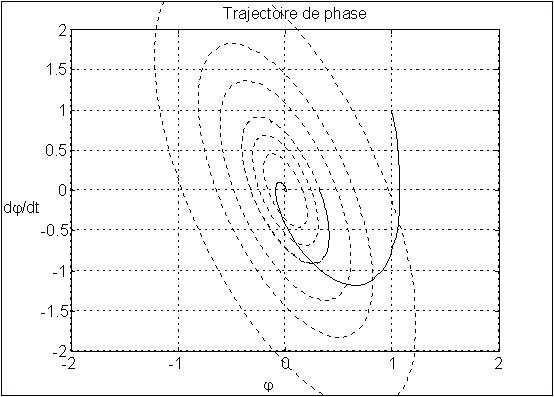
Les trajectoires de notre système dans le repère
initial ![]() sont
des "spirales logarithmiques elliptiques" (cette terminologie n'est pas
académique !) ; un exemple de trajectoire coupant les ellipses "équidistance"
est représentée ci-dessous :
sont
des "spirales logarithmiques elliptiques" (cette terminologie n'est pas
académique !) ; un exemple de trajectoire coupant les ellipses "équidistance"
est représentée ci-dessous :
Revenons à présent au système non linéaire d'origine, sujet de notre étude. La première équation a un point d'équilibre en :
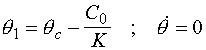
La seconde équation a un point d'équilibre en :
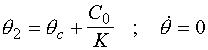
La troisième équation admet tout l'axe ![]() comme équilibre.
comme équilibre.
Chacune de ces équations détermine une famille de trajectoires, la commutation de l'une des familles vers une autre étant déterminée par le passage à la vitesse nulle. Si la vitesse s'annule pour q1 < q < q2 , alors la vitesse reste nulle, et le système est bloqué dans la troisième équation. Le couple moteur ne peut compenser le frottement sec, il y a arrêt du système même si l'erreur de position n'est pas nulle.
Cette erreur est aléatoire si l'état initial est aléatoire.
Une trajectoire est représentée ci-dessous :
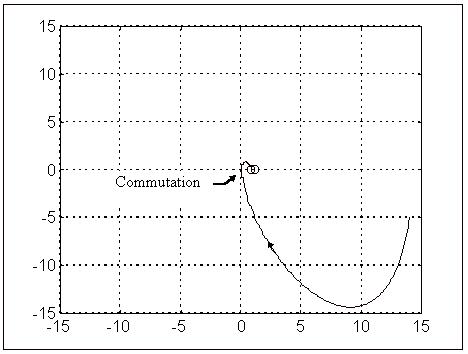
La trajectoire aux derniers instants du mouvement apparaît comme prévu :
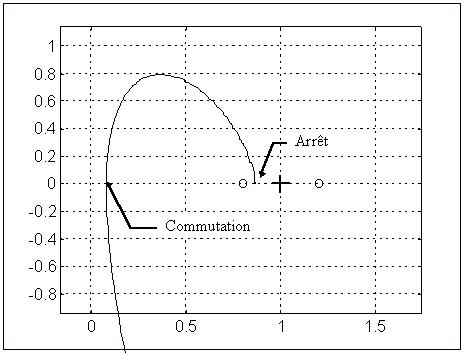
Le frottement sec était : C0 = 0.02 N.m , le point de consigne (1,0), le gain K=0.1 , ce qui détermine le segment d'arrêt : 0.8 < q < 1.2
Une autre illustration est donnée ci-dessous ; elle concerne le cas sans frottement, c'est à dire celui d'un système non dissipatif, dont les trajectoires libres sont fermées (aucun amortissement ne rapproche le mobile de l'origine). Ces trajectoires sont des ellipses, mais on a pris pour l'illustration :
inertie J=1 frottement f=0 gain K=1
ce qui donne des trajectoires circulaires.
La consigne est choisie égale à : qc = 1 et le couple de frottement sec C0 = 2, ce qui donne un arrêt du système sur l'intervalle [-1 ; 3].
Les trajectoires sont des cercles centrés soit sur (-1,0) , soit sur (3,0). C'est ce qu'illustre la figure suivante, on l'on constate la commutation d'une famille de trajectoires à l'autre au passage à vitesse nulle et l'arrêt en un point dépendant de l'état initial.
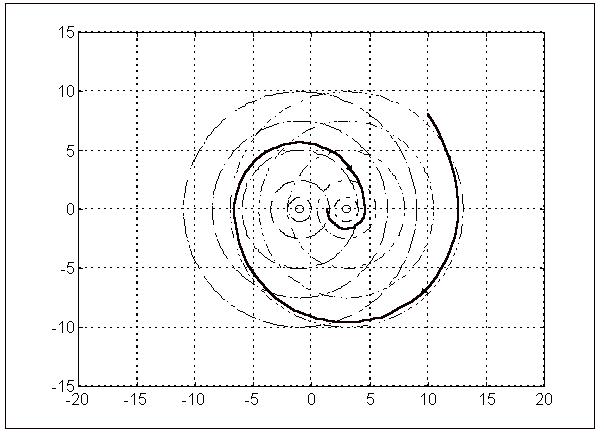
Fin
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec