"L'information véhiculée par un signal dont le spectre est à support borné n'est pas modifiée par l'opération d'échantillonnage à condition que la fréquence d'échantillonnage soit au moins deux fois plus grande que la plus grande fréquence contenue dans le signal.

La reconstitution du signal original peut être effectuée par un filtre passe-bas idéal de fréquence de coupure égale à la moitié de la fréquence d'échantillonnage."

Démontrons ce théorème.

Soit f(t) un signal dont le spectre est à support borné :

Notons tout de suite que le module du spectre d'un signal à valeurs réelles est une fonction paire de la fréquence, ce qui justifie la symétrie en "w" de la condition.

Illustration :

Le signal échantillonné à la cadence T_e est (cf : polycopié "échantillonnage") :

Son spectre est :

Cette expression exprime la répétition périodique du spectre. On peut aussi écrire la transformée de Fourier du signal échantillonné sous la forme :

Or, le fait que F(w) soit à support borné nous autorise à écrire :

sous la condition que : w_e - w_max > w_max , soit : w_e > 2. W_max (condition de Shannon)

Illustration :

On peut écrire la transformée inverse de Fourier de F(w): 

Et aussi en vertu de (3) :

L'intégrale se calcule aisément et vaut 2.w_max . sinc [w_max.(t-n.T_e)] , ce qui donne pour f(t) :

Cette dernière égalité signifie que f(t) est entièrement déterminé par la connaissance de ses échantillons (en nombre infini ...) aux instants n.T_e et que la fonction sinus cardinal sert à relier les échantillons ; on l'appelle parfois "fonction d'interpolation de Shannon". Il n'y a donc pas de perte d'information si (et seulement si) l'on possède tous les échantillons ; ceci est le cas puisqu'on possède f^*(t) après l'opération d'échantillonnage.

Afin de générer les fonctions sinus cardinal, il suffit de filtrer le signal f^*(t) , qui est une suite d'impulsions, par un filtre dont la réponse impulsionnelle est un sinus cardinal. Un tel filtre est bien connu : il s'agit du passe-bas idéal. On obtiendra en sortie une reconstruction de f(t), à une constante multiplicative près, et à un retard près. Ce filtre n'est malheureusement pas causal, et donc est irréalisable en temps réel, mais on peut bien sûr l'approcher ; c'est ce qui est fait dans toute opération de reconstruction, à l'aide d'un filtre interpolateur. (Les signaux à spectre à support borné sont de durée infinie, ce qui les exclut d'emblée de toute expérimentation : on les approche par des signaux de durée suffisante.)
 
 

Illustration : un signal original (-) comportant une composante à 1 rd/s et une autre à 1,5 rd/s est échantillonné à quatre fois 1,5 rd/s.

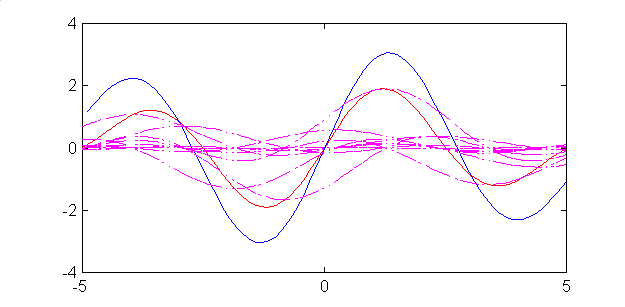
Les différents sinus cardinaux (--) pondérés par l'échantillon correspondant sont ajoutés pour reconstituer (-) le signal. On peut noter une distorsion, dûe bien sûr à la durée finie de la simulation.

Script Matlab de génération de l'image ci-dessus

Construction de la "base" de sinus cardinaux .

t=-5:0.1:5;, y=sin(t)+sin(1.5*t);

wm=1.5;  , we=4*wm;, Te=2*pi/we; ,   tt=-5:Te:5;

yy=interp1(t,y,tt,'spline');

ysinc=[];

for k=1:10,yyk=yy(k);,ttk=tt(k);,ysinc=[ysinc yyk*sin(wm*(t'-ttk))./(wm*(t'-ttk))];,end

figure,plot(t,y,'-r',t,sum(ysinc'),'-b',t,ysinc,'--m'),grid on

Un dernier mot : il a été dit que l'échantillonnage vu précédemment ne perdait pas d'information. On constatera pourtant que l'échantillonnage d'un signal à spectre passe-bande étroit donne, une fois reconstruit par un filtre passe-bas, un signal qui se situe dans une bande différente de fréquences. Mais ceci ne modifie pas le contenu informationnel, ce qui rejoint à l'évidence les notions de transposition de fréquence utilisées en transmission. De même, la stroboscopie déplace le spectre sans forcément diminuer la quantité d'information (elle la rend même plus "lisible" à nos yeux).

Consulter la bibliographie

Retour à la page d'accueil