![]() (1)
(1)
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec
Commande par modes glissants
(«Sliding modes»)
Résumé : Ici, on présente succinctement le principe de la commande par modes glissants, sur l'exemple désormais classique d'un double intégrateur. Puis cette technique est appliquée à la commande en position d'un moteur pas-à-pas. Deux lois de commande sont développées, et des résultats expérimentaux sont présentés.
Introduction
Les modes glissants constituent une manière simple et robuste de réglage des systèmes automatiques. L'application aux actionneurs électromagnétiques ne représente qu'un cas particulier, cette technique connaissant des développements importants dans tous les domaines de la commande. Aussi allons-nous présenter le principe des modes glissants à partir d'un système générique : l'intégrateur double, qui modélise par exemple la position d'une masse actionnée par une force.
2.Recherche d'une commande assurant un mode glissant
3.Application à un moteur pas-à-pas
Notion de glissement
Considérons le système suivant :
![]() (1)
(1)
où x est la position d'un mobile, u la force appliquée, et Cr une force de résistance quelconque.
Si la commande est du type tout ou rien, alors
u = +/- U, et les trajectoires sont données par :
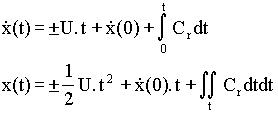 (2)
(2)
Pour Cr=0, ce sont des paraboles dans le plan ![]() .
.
L'objectif de commande étant maintenant de ramener x à l'origine, on constate que la commande bouclée avec retour de la seule position :
u = -U.sign(x) (3)
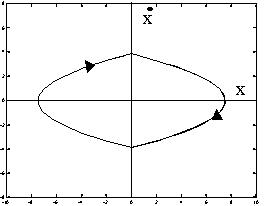
ne permet pas de stabiliser le système, les trajectoires en l'absence de force résistante étant périodiques, comme on peut voir sur la figure I. Il vaut mieux utiliser un retour de la forme [1]:
![]() (4)
(4)
qui donne la convergence (figure II).
 |
 |
| Figure I : commande par retour de position | Figure II : retour de position et de vitesse |
| La droite |
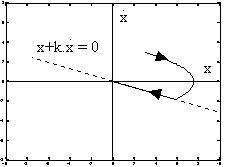 |
| Figure III : glissement |
Recherche d'une commande assurant un mode glissant
La commande de la figure III a longtemps
été jugée néfaste, par les effets de réticence
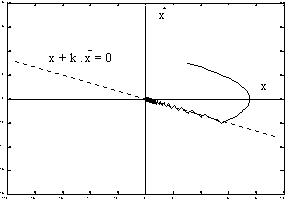
dûs aux retards de commutation (figures IV et V) : la commande était
jugée brutale et peu efficace, sollicitant fortement les organes
de commande.
 |
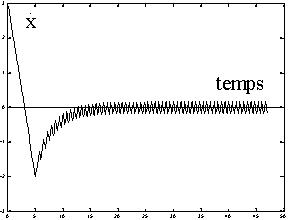 |
| Figure IV : réticence | Figure V : réticence, allure de la vitesse |
Pourtant, comme nous allons le voir, les trajectoires obtenues sont largement insensibles aux perturbations, et la dynamique du procédé peut être choisie avec une grande liberté. Notons pour l'instant que la commande tout ou rien présente l'intérêt remarquable d'être plus rapide qu'une commande linéaire bornée.
Choisissons, assez arbitrairement d'ailleurs, une courbe de commutation. Par exemple, la droite
![]() définie
plus haut :
définie
plus haut :
D : ![]()
Le but que nous recherchons est le suivant : rejoindre
à partir de l'état initial la droite ![]() ,
puis astreindre la trajectoire à rester sur cette droite. Alors,
la dynamique du système sera fixée par l'équation
de la droite, et l'origine sera rejointe avec la constante de temps
k.
,
puis astreindre la trajectoire à rester sur cette droite. Alors,
la dynamique du système sera fixée par l'équation
de la droite, et l'origine sera rejointe avec la constante de temps
k.
Posons donc : S =![]() (5)
(5)
En dérivant, il vient :
![]() (6)
(6)
Lorsque Cr est nul, la commande :
ue = ![]() (7)
(7)
garantit ![]() = 0, ce qui signifie que la trajectoire est contrainte à demeurer
sur la droite S sur laquelle elle se trouve. Cette droite est donc invariante
en l'absence de perturbation. ue est appelée "
commande équivalente ".
= 0, ce qui signifie que la trajectoire est contrainte à demeurer
sur la droite S sur laquelle elle se trouve. Cette droite est donc invariante
en l'absence de perturbation. ue est appelée "
commande équivalente ".
Afin d'obliger le système à suivre la trajectoire imposée, il suffit à présent de rendre S = 0 attractive. Pour cela, on ajoute une commande commutante uc à la commande équivalente ue sous la forme :
uc = -V.sign (S) (8)
u = u e + uc (9)
En choisissant V assez grand :
V > ![]() (10)
(10)
alors la condition S. ![]() < 0 est toujours réalisée, ce qui prouve que S = 0 est
attractive et invariante, malgré Cr .
< 0 est toujours réalisée, ce qui prouve que S = 0 est
attractive et invariante, malgré Cr .
*
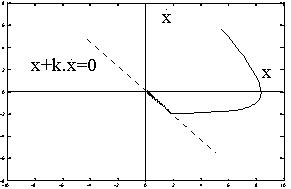
Le résultat obtenu avec la commande (9) est illustré
sur les figures VI et VII. On peut y observer le ralliement de l'origine
avec une dynamique du premier ordre, donnée par la valeur de k.
 |
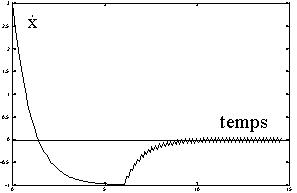 |
| Figure VI | Figure VII |
Cette commande présente les caractéristiques suivantes :
- elle est robuste, rejetant la perturbation Cr.
- il suffit de connaître une borne pour Cr, ce qui simplifie le réglage.
- le choix de la surface de commutation est assez libre.
- la commande est adoucie par la présence de la commande équivalente ; celle-ci peut cependant être supprimée, au prix d'une augmentation de V.
- on a en quelque sorte les avantages d'un système à grand gain, sans en avoir les inconvénients.
- on peut étendre la technique à des surfaces autres que des droites, de dimensions quelconques, et à des intersections d'autant de telles surfaces qu'on a de commandes disponibles.
- nulle part on n'a postulé la linéarité du système ; ce principe est utilisable avec des systèmes non-linéaires.
- on n'a pas parlé de pôles, la convergence étant prouvée par un argument élémentaire.
-on n'a pas non plus parlé de marge de stabilité, la condition (10) en tenant lieu.
De nombreuses variantes existent, visant à limiter l'effet de réticence et à optimiser les trajectoires de commande, ainsi qu'à lever les difficultés théoriques liées aux discontinuités de commande. (voir [2],[3] ).
Application à un moteur pas-à-pas
Les moteurs pas-à-pas jouent un rôle important parmi les actionneurs électriques. En effet, ils permettent le positionnement en boucle ouverte. Mais au delà de cette justification, qui limite les possibilités de précision, les moteurs pas-à-pas sont des actionneurs sans balais capables d'un couple important sans réducteur mécanique.
Ici, nous considérons un moteur à aimant permanent, à force contre-électromotrice sinusoïdale [4], et l'objectif que nous nous fixons est le pilotage en position. La précision obtenue devra être indépendante de la résolution du moteur (" nombre de pas par tour "). Nous supposons de plus que l'état est mesuré : capteurs de courant et capteur de position angulaire. Aucune hypothèse n'est faite, en revanche, sur la technologie du pré-actionneur, amplificateur linéaire ou commutateur : il s'agit simplement d'une commande en tension.
Le moteur est biphasé (ou tétraphasé avec point milieu).
Le modèle du moteur s'écrit, dans un repère a-b lié au stator :
L ![]() = va -R ia+ K W sin( N
= va -R ia+ K W sin( N![]() )
)
L ![]() = vb -R ib - K W cos( N
= vb -R ib - K W cos( N![]() )
(M1)
)
(M1)
J![]() = K (ib
cosN
= K (ib
cosN![]() -
ia sinN
-
ia sinN![]() )
+ Cr
)
+ Cr
![]() = W
= W
ia, ib : intensités dans les phases a et b
va, vb : tensions aux bornes des phases a et b, considérées comme grandeurs de commande.
![]() ,
, ![]() : vitesse et position angulaires du rotor
: vitesse et position angulaires du rotor
N : nombre de dents du rotor (e.g. 50 dents pour 200 pas par tour)
J : moment d'inertie ramené à l'arbre
R : résistance d'une phase statorique
L : inductance d'une phase statorique
K : coefficient de force électromotrice / coefficient de couple
Cr : couple de perturbation
Ce modèle néglige la variation de réluctance liée à la rotation, et inclus le couple de détente
- en sin( 4N![]() )
- dans Cr. Il est tout à fait semblable au modèle
de la machine synchrone à aimant permanent à pôles
lisses. (Pour des détails, voir [5] par exemple).
)
- dans Cr. Il est tout à fait semblable au modèle
de la machine synchrone à aimant permanent à pôles
lisses. (Pour des détails, voir [5] par exemple).
Dans un premier temps, on va chercher à commander la vitesse de rotation W par mode glissant. Après application de la transformation de coordonnées
| cos
(N. |
sin
(N. |
||||
| T = | (11) | ||||
| - sin(N. |
cos (N. |
on peut exprimer les courants et tensions dans le repère d-q tournant lié au rotor : vdq = T. vab ; vab = T-1. vdq
idq = T. iab ; iab = T-1. idq
et le modèle s'exprime sous la forme :
L ![]() = vd - R id + N L
= vd - R id + N L![]() iq
iq
L ![]() = vq - R iq - N L
= vq - R iq - N L![]() id - K
id - K![]()
J![]()
![]() = K iq + Cr (M2)
= K iq + Cr (M2)
![]()
![]() =
= ![]()
On définit aussi une trajectoire de référence obéissant au modèle, sous la forme :
L ![]() = vdr - R idr + N L
= vdr - R idr + N L ![]() r
iqr
r
iqr
L ![]() = vqr - R iqr - N L
= vqr - R iqr - N L![]() idr - K
idr - K ![]() r
r
J![]()
![]() r
= K iqr (M2r)
r
= K iqr (M2r)
![]()
![]() r
=
r
= ![]() r
r
les indices r valant pour " référence ". L'élaboration des trajectoires de référence est détaillée dans [6].
Posant e = [id-idr iq-iqr![]() -
-![]() r
]T = [x1 x2 x3
]T
r
]T = [x1 x2 x3
]T
et : Dvd = vd - vdr ; Dvq = vq - vqr
le modèle de l'écart entre la référence et la trajectoire réelle est :
L ![]() = Dvd - R x1 + N L (
= Dvd - R x1 + N L (![]() iq -
iq - ![]() r
iqr)
r
iqr)
L ![]() = Dvq -R x2 -N L (
= Dvq -R x2 -N L (![]() id -
id - ![]() r
idr) - K x3
r
idr) - K x3
J![]() = K x2 + Cr (M2e)
= K x2 + Cr (M2e)
Considérons la surface suivante dans l'espace d'état
: S = k x3 + ![]() (12)
(12)
La condition S = 0 signifie que![]() converge exponentiellement vers sa référence.
converge exponentiellement vers sa référence.
Calculant la dérivée de S par rapport au temps:
![]() (13)
(13)
on obtient :
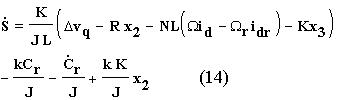
expression pour laquelle la commande :
Dvqe=K x3 +(R -k L)x2
+NL(![]() id
-
id
-![]() r
idr) (15)
r
idr) (15)
garantit ![]() =
0 en l'absence de la perturbation Cr et de sa dérivée
. Ainsi, en l'absence de perturbation, la surface S est positivement
invariante.
=
0 en l'absence de la perturbation Cr et de sa dérivée
. Ainsi, en l'absence de perturbation, la surface S est positivement
invariante.
Afin d'assurer l'attractivité de la surface S = 0, on complète la commande (15) par une commande à deux états vqc sous la forme :
Dvq = Dvqe + vqc(16)
L'utilisation de cette commande conduit à :
![]() =
= ![]() vqc +
vqc + 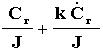 (17)
(17)
Prenant vqc = - U0 sign(S), la
condition S.![]() <0
peut être imposée pour S ¹ 0 en choisissant U0
suffisamment grand :
<0
peut être imposée pour S ¹ 0 en choisissant U0
suffisamment grand :
U0 > 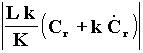 (18)
(18)
Cette inégalité garantit l'attractivité de la surface S = 0 en présence de la perturbation Cr - à condition que cette perturbation soit bornée, ainsi que sa dérivée - .
Ainsi, toute trajectoire converge vers S = 0 en temps fini, puis est confinée sur cette surface, et la vitesse converge bien vers sa référence.
La commande complète de vq est donnée finalement ainsi :
vq = vqr + K x3 +
(R - k L) x2 + NL(![]() id -
id - ![]() r
idr) - U0.sign(S) (19)
r
idr) - U0.sign(S) (19)
On peut choisir d'imposer vd = 0, ce qui revient à un pilotage en quadrature - lequel n'est possible qu'en autopilotage -. Les tensions de commande sont alors élaborées à partir de la transformation inverse des coordonnées T-1.
La vitesse étant ainsi réglée, le réglage de la position peut être obtenu avec un correcteur PI par exemple.
'
Une autre possibilité, parmi les nombreuses voies utilisables, est de régler directement les courants dans le repère fixe du stator. On cherche donc à garantir la poursuite des trajectoires de courant dans le repère a-b, c'est à dire :
ia -> iar
ib -> ibr
Prenons comme surfaces de glissement :
Sa = ia - iar (20)
Sb = ib - ibr (21)
La dérivée par rapport au temps de Sa est :
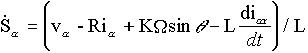 (22)
(22)
qui s'annule pour une commande vae :
![]() (23)
(23)
Ainsi, la commande vae garantit l'invariance positive de S. L'attractivité de S = 0 est obtenue par :
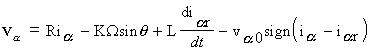 va0
>
0 (24)
va0
>
0 (24)
qui garantit : ![]()
De la même manière, on obtient pour le courant dans la phase b :
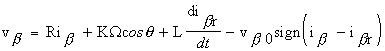 vb0
>
0 (25)
vb0
>
0 (25)
qui garantit : ![]()
Ainsi, les courants suivent leurs références. On peut ensuite imposer ces références pour obtenir un couple moteur garantissant la poursuite de trajectoire de position ou de vitesse. Le plus simple est de déterminer id et iq assurant ce couple, puis d'extraire iar et ibr par transformation inverse de coordonnées T-1.
Un choix possible consiste à prendre id = 0 , iq étant obtenu par un correcteur PI sur la position.
'
Résultats expérimentaux ; noter que la consigne ne correspond pas à un nombre entier de pas : la précision est indépendante de la résolution du moteur.
N.B.: Tech = 2 ms, le dispositif utilisé ne permet pas d'aller plus vite ...
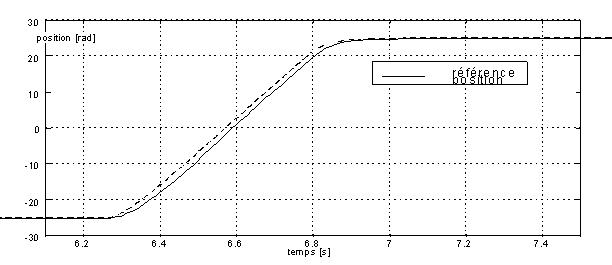
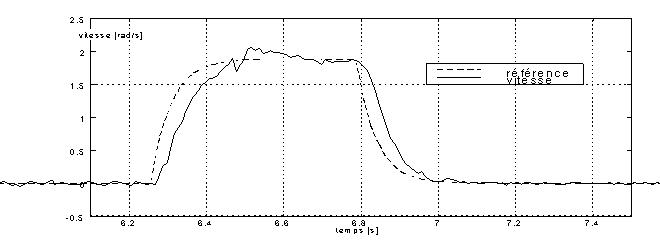
Figure X : résultats pour la commande (19)
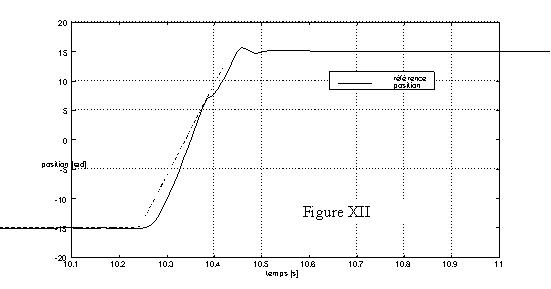
La commande en position utilisant les lois (24) et (25), dans laquelle le courant transverse de référence, iqr , est élaboré par un correcteur PI sur la position, est illustrée sur les figures XI et XII.
Références :
[1] : J.Ch.Gille, P.Decaulne, M.Pélegrin Systèmes asservis non linéaires Editions Dunod 1988
[2] : V.I.Utkin Sliding mode control design principles and applications to electric drives
IEEE Transactions on industrial electronics Vol. 40 n° 1 Février 1993
[3] : H.Sira-Ramirez Dynamical sliding mode control of nonlinear systems Int. Journal of Control 1993 vol.57 n° 5
[4] : G.Grellet ; G.Clerc Les actionneurs électriques Editions Eyrolles 1998
[5] : J.P.Caron ; J.P.Hautier Modélisation et commande de la machine synchrone
Journées de l'Enseignement de l'Electrotechnique et de l'Electronique Industrielle, SEE, 1995
[6] : A.Rachid Régulation électromécanique Techniques de l'ingénieur R7-540
retour en haut de la page - retour
à la page d'accueil - voir la bibliographie
générale
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes glissants - Conversion sigma-delta - Modulation AM - Commande avec frottement sec