 - TS Electrotechnique
- TS Electrotechnique
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes
glissants - Conversion sigma-delta - Modulation AM - Commande avec
frottement sec
Approche de l’automatique non-linéaire par les méthodes de Lyapunov
II. Approche globale : fonctions de Lyapunov
II.1 L’analogie mécanique
Considérons par exemple un pendule pesant ou un système à ressorts : l’intégration du modèle non linéaire est difficile, ou même impossible. Cependant, un résultat certain apparaît lorsqu’on s’intéresse à l’énergie mécanique emmagasinée dans le système : c’est une fonction qui décroît avec le temps, ce qui conduit finalement à l’immobilisation du système.
A quoi est due cette décroissance ? Elle est due à la dissipation d’énergie liée aux frottements, ou plus généralement à la non réversibilité des phénomènes de transport et de transformation de l’énergie.
Ainsi, dans les systèmes dissipatifs, l’énergie décroît, et le système est stable quelquepart. Un cas limite est celui des systèmes conservatifs – i.e. " sans frottement " - qui peuvent rester éternellement en dehors de l’équilibre.
Bien entendu, il faudra se méfier des systèmes dans lesquels l’énergie peut augmenter par un apport extérieur.
Exemple du pendule pesant:
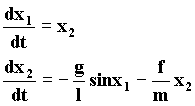
avec g : accélération de la pesanteur
l : longueur du balancier
f : coefficient de frottement visqueux
m : masse
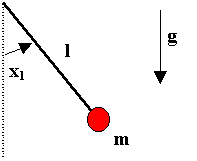
On vérifie sans peine que [x1 ; x2] = [2.k.pi ; 0] sont des points d’équilibre, stables localement en vertu du premier théorème de Lyapunov.
Définissons la fonction énergie E en ajoutant l’énergie cinétique et l’énergie potentielle :
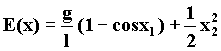
positive ou nulle, et calculons sa variation au cours du temps :
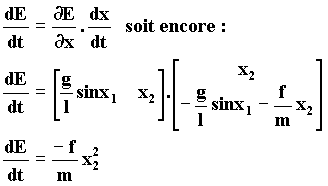
La variation d’énergie est toujours négative dès qu’il y a mouvement, le système est donc stable (chaque mouvement diminue l’énergie, et il s’arrêtera en un point d’énergie minimum).
II.2 Seconde méthode de Lyapunov
Ce qui précède se formalise de la manière suivante :
Théorème n°2
Soit x= xe un point d’équilibre, et D un domaine entourant l’équilibre.
Si il existe une fonction dérivable V(x) telle que :
V(0) = 0
V(x) > 0 pour x ¹ 0
Alors, l’équilibre est stable si ¶ V/¶ t [ 0 dans le domaine D
et asymptotiquement stable si ¶ V/¶ t = 0 seulement en x = xe.
La méthode est alors la suivante :
a. Pour pouver la stabilité d’un équilibre, on recherche une fonction positive de l’état dont la dérivée dans le temps est négative.
b. Si une fonction positive possède une dérivée temporelle non-négative, alors on ne peut rien conclure.
II.3 Retour sur le pendule pesant
Considérons pour le pendule, étudié pour |x1| < pi, la fonction :
V(x) = ½.xTPx + (g/l)(1-cosx1)
avec : 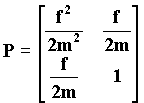
La fonction V(x) est évidemment positive, puisque P est définie positive. Sa dérivée est :
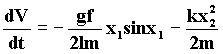
qui est négative, et nulle seulement en x = [0 ; 0] . L’équilibre est donc asymptotiquement stable.
(Cet exemple est détaillé dans le livre de Khalil cité en bibliographie).
II.4 Recherche de fonctions de Lyapunov
La recherche d’une fonction satisfaisant les conditions ci-dessus est parfois délicate, la découverte d’une telle fonction n’est pas garantie.
En général, on commence par essayer des fonctions quadratiques de l’état
V(x) = xTPx , P définie positive.
D’autres fonctions, comportant des intégrales, sont aussi employées. En règle générale, on cherche une fonction " candidate " avec un nombre suffisant de paramètres pour pouvoir rendre sa dérivée négative. Ce sujet sera abordé à propos de la commande par les fonctions de Lyapunov.
II.5 Lignes de niveau d’une fonction de Lyapunov
A titre d’illustration, on va représenter dV/dt pour l’exemple d’un système linéaire défini par :
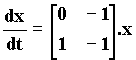
pour lequel la fonction V(x) = 1,5 x12 – x1x2 + x22 est une fonction de Lyapunov.
La réponse libre dans le plan de phase est représentée en superposition avec les " lignes de niveau " de V(x) ; on constate que la trajectoire du système évolue toujours vers des niveaux inférieurs, ce qui traduit le fait que dV/dt < 0
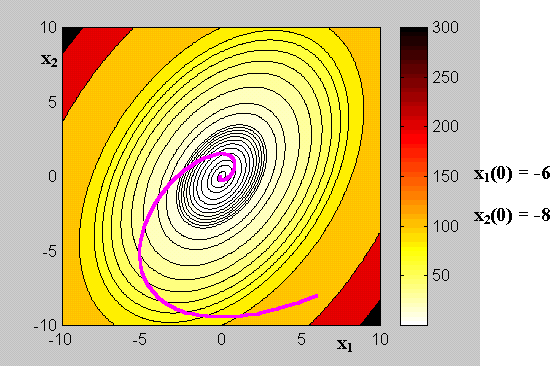
Note : pour un système linéaire stable dx/dt = A . x , une fonction de Lyapunov peut être trouvée à coup sûr sous la forme V(x) = xT P x, P étant solution de l’équation P A + AT P = -I (" équation de Lyapunov ").
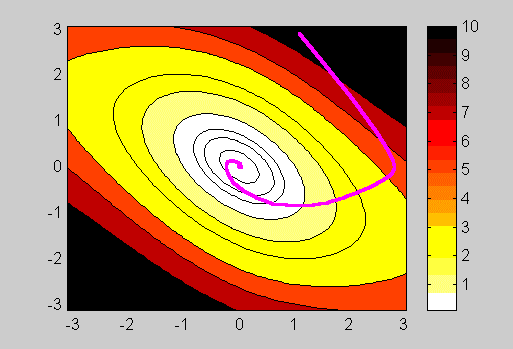
Pour le pendule pesant, avec la fonction proposée au paragraphe II.3, une trajectoire traversant les lignes de niveau en descendant est représentée de la même manière :
 - TS Electrotechnique
- TS Electrotechnique
- Des livres à lire - Nouveau Livre ! - Liens et adresses -
Shanon - Contrôle prédictif - Lyapunov - DSP - Filtre RIF
Modes
glissants - Conversion sigma-delta - Modulation AM - Commande avec
frottement sec