.

Résistances ( Résistor)

code des couleurs, construction, couplage, comportement thermique (coéficient de température), comportement en fréquences

Définitions
Le terme "résistance" est utilisé autan pour décrire l'opposition faite au passage du courant par un fil (on parle de la résistance d'un fil.) que pour nommer un élément (dipôle) qui en électricité ne crée pas de déphasage courant - tension; dont la puissance absorbée ne change pas pour une alimentation continue ou alternative de même valeur (appelé parfois résistor).

Lorsqu'on parle de la résistance d'un fil, sa valeur est définie par la résistivité du matériau de l'âme de ce conducteur, sa longueur et sa section.

R = r * longueur / section    [W]

Sa puissance est toujours une puissance active . donc le produit U_R . I_R = U_Z . I_Z . cos f.    [W]

Code des couleurs :

En électronique les résistances sont de petits cylindres de différents diamètres selon la puissance sur lesquels sont inscrits des cercles de couleurs. Ces couleurs permettent de connaître la valeur de la résistance ainsi que sa tolérance.

Ainsi une résistance qui a des bandes de couleurs "bleu - rouge - jaune - brun"

indique une résistance comprise entre   613 800 et 626 200  ohms (620 000 ohms ± 1 %)

construction:

• Les résistances bobinées (de quelques ohms à quelques milliers d’ohms) sont constituées d’un fil en alliage (nickel-chrome ou cuivre-nickel pour des résistances de haute précision à faible coefficient de température) enroulé sur un support isolant en céramique ou en matière plastique.

• Les résistances à feuilles métalliques (de quelques ohms à quelques megaohms) sont des résistances très précises, constituées d’une feuille en alliage (souvent du nickel-chrome) fixée sur un substrat isolant.
• Les résistances agglomérées (de quelques ohms à quelques méga ohms) sont formées d’un mélange de carbone, de matière isolante et de liant (par exemple de la bakélite.). Le pourcentage de carbone détermine la valeur de la résistance. Les caractéristiques obtenues sont très moyennes, mais la fiabilité ainsi que le faible coût de ces résistances en font des composants couramment employés dans les montages électroniques.
• Les résistances à couches métallique, l’élément résistant est obtenu par la pose d'une couche d'env. 0,1mm d’un alliage sur un substrat en céramique ou en quartz.. Ce type de résistances a un petit coefficient de température.
• Les résistances à couches de carbone se font par pyrolyse en atmosphère d’hydrocarbure (méthane, butane ou benzène) et d’argon. le carbone se dépose sur de petits bâtons  isolant servant de support.
• les résistances à couches épaisses (> 1 méga ohm) sont faites d’une pâte de verres fusibles et de métaux nobles déposée (quelques dizaines de µm) par sérigraphie sur un support d’alumine, puis cuite à haute température.

Couplages

- La valeur de la résistance équivalente de plusieurs résistances placées en série est égale à la somme des valeurs de chacune des résistances.

R_équivalent = R₁ + R₂ + R₃ + ..... + R_n(  [W] unité : l'ohm)

note : un couplage série est un couplage de deux (ou plus) composant relies électriquement sans nœuds entre eux ( sur la même branche).

- La valeur de la résistance équivalente de plusieurs résistances placées en parallèle est égale à l'inverse de la somme des inverses des valeurs de chacune des résistances.

R_équivalent = 1/ (1/R₁ + 1/R₂ + 1/R₃ + ..... + 1/R_n)    [W]( unité : l'ohm)

note : un couplage parallèle est un couplage de deux (ou plus) composant reliés à chacune de leurs extrémités aux mêmes potentiels ( au mêmes nœuds).

note 1 : Dans ce cas la valeur de la résistance équivalente est plus petite que n'importe quelle valeur de résistance faisant partie du couplage.
note 2 : Pour ce couplage, il est préférable d'utiliser la conductance des résistances car la conductance équivalente est égale à la somme des conductances.

G_équivalent = G₁ + G₂ + G₃ + ..... + G_n     [S]    ( unité : le siemens - S)

- Lorsqu'on ne peut pas transformer un circuit mixte en couplage parallèle ou série , on peut utiliser les transformations étoile - triangle  ou triangle - étoile ( circuit monophasé avec 3 nœuds de connections).

Comportement thermique

Habituellement, on l'utilise directement avec la résistance ce qui nous donne comme formules :

Supraconduction.

A très basse température, les métaux purs (0K ou -273 °C-) perdent leur résistance électrique.

La recherche à permis de trouver des alliages métalliques (par exemple le niobium) qui est supraconducteur à "seulement" -250°C. A la fin du siècle passé (env. 1980-1990), ont fait des alliages d'oxydes qui peuvent travailler à -190°C -ce qui est la température de l'azote liquide et donc permet de diminuer le coût .

Comportement en fréquence :

On admet que la valeur de la résistance ne change pas si la fréquence varie. Toutefois, pour des fréquences très élevées  (MHz, GHz), on constate un effet pelliculaire ( les électrons libres sont repoussés en périphérie du conducteur) ce qui diminue la surface de conduction et  augmente donc la résistance.

Dans les têtes de télé réseaux, les conducteurs ( guides d'ondes) sont creux.

L'inductance

Définition

Une inductance est un effet électromagnétique - l'induction et la self induction - dans un appareillage électrique (conducteurs, bobine, etc..). Son symbole est L et son unité H.
L'inductance présente une réactance d'induction - qui est sa valeur ohmique -   lorsqu'elle est alimentée par une tension électrique. Cette réactance a comme particularité de créer un déphasage courant - tension de 90 degrés.

Dans une inductance le courant est en retard par rapport à la tension.

La réactance d'induction (X_l) dépend de la vitesse de variation du flux magnétique, sa valeur dépend donc directement de la fréquence.

X_l = 2 . p . f . L   [W]

On peut en conclure qu'à une fréquence nulle (tension continue lisse) X_l = 0 ohm et que plus la fréquence augmente, plus sa valeur ohmique augmente.

Ci-dessous la caractéristique de X_l en fonction de la fréquence (pour L = 1 mH).

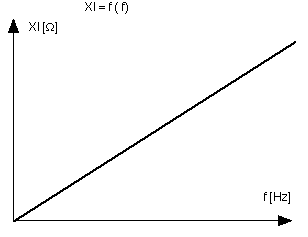
Sa puissance est toujours une puissance réactive donc le produit Q_l =U_X . I_X = U_Z . I_Z . sin f    [var]

note : Une bobine n'est jamais une inductance pure donc elle se modélise avec une résistance et une inductance pure placée en série. Son impédance sera donc la somme vectorielle (ou géométrique) de sa résistance et de sa réactance d'induction.

Attention: lors d'une mesure à l'ohmmètre d'un bobinage, la valeur mesurée est sa résistance et non son impédance.

Couplage de réactances d'induction pures

- La valeur de la réactance d'induction équivalente de réactances d'induction placées en série est égale à la somme des valeurs de chacune des réactances.

X_{l équivalent} = X_{l 1} + X_{l 2} + X_{l 3} + ..... + X_{l n}   [W] ( unité : l'ohm)

- La valeur de la réactance d'induction équivalente de réactances d'induction placées en parallèle est égale à l'inverse de la somme des inverses des valeurs de chacune des réactance d'induction.

X_{l équivalent} = 1/ (1/ X_{l 1} + 1/ X_{l 2} + 1/ X_{l 3} + ..... + 1/ X_{l n})   [W]( unité : l'ohm)

note 1 : Dans ce cas la valeur de la réactance d'induction équivalente est plus petite que n'importe quelle valeur de réactance d'induction faisant partie du couplage.

LA LOI D'OHM:

La loi d'ohm exprime le rapport qu'il existe entre la tension, le courant et l'impédance (résistance si alimenté en tension continue) soit :

Z=U/I       [W]          U=Z*I      [V]               I=U/Z   [A]

Ces différents rapports sont valables pour les circuits à courant continu et les circuits alternatifs monophasés. Toutefois on peut très bien - et c'est vivement recommandé de le faire - adapter ces rapports à tous les circuits à impédance ( voir circuits RL , RC et RLC) avec, de manière générale,  les rapports suivant:

R = U_R / I_R   [W] (avec U_R = tension aux bornes de la résistance et I_R = intensité du (vecteur) courant à travers cette même résistance)

X_c = U_xc / I_xc    [W] (avec U_xc = tension aux bornes de la réactance de capacité et I_xc = intensité du  (vecteur) courant à travers ce même élément)

X_l = U_xl / I_xl   [W] (avec U_xl = tension aux bornes de la réactance d'induction et I_xl = intensité du (vecteur) courant à travers ce même élément)

Dans un circuit composé de deux impédances en série, cette loi nous permet de définir un diviseur de tension:

Soit Z₁ et Z₂ en série raccordés à une source de tension U continue.
le courant vaut : I= U / (Z₁+Z₂)     [A]

la tension aux bornes de Z₁ vaut : U₁ = Z₁*I₁ soit U₁ = Z₁ * U / (Z₁+Z₂)  [V]
la tension aux bornes de Z₂ vaut : U₂ = Z₂*I₂ soit U₂ = Z₂ * U / (Z₁+Z₂)   [V]

voir les calculs selon la loi d'ohm...

LES CIRCUITS RL

Dans les circuits RL nous allons voir d'abord le couplage RL série puis le couplage RL parallèle

Le circuit RL série est composé d'une résistance purement ohmique et d'une inductance (self, bobine, enroulement de moteur, etc.) pure. A noter qu'une inductance non pure se modélise avec un circuit RL série dont la résistance est celle du fil constituant la bobine. Pour plus de renseignements à ce sujet, revoir la théorie des inductances

Le circuit RL série a une caractéristique globale pour laisser bloquer le courant qui se nomme impédance.

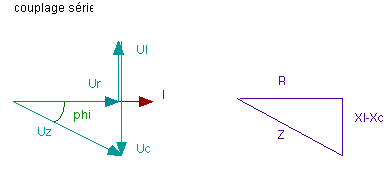
Principales caractéristiques de ce montage:
    - le courant est le même pour les trois éléments - R, X_l,Z
    - les tensions sont différentes:
        a) U_r est en phase avec I
        b) U_l est en avance de 90 degrés par rapport à I
        c) U_z - aussi tension d'alimentation - présente un décalage compris entre 0 et 90 degrés.
    - le circuit est dit inductif.

Le calcul de l'impédance de ce montage peut se faire soit en utilisant le rapport

Z = U_z/I_z      [W]
soit avec Pythagore Z= ( R² + X_l² ) ^0,5   [W]  

     (note puissance 0,5 = racine carré de..)

note: Les distributeurs d'énergie électrique imposent des valeurs minimales du cos f. Pour améliorer ce facteur, il faut compenser l'énergie inductive par de l'énergie capacitive fournie par des condensateurs (pour les "petits récepteurs - p. ex. armature TL) ou par des moteurs synchrones surexcités (pour les réseaux de distribution).

exercices RL série

LES CIRCUIT RL PARALLÈLE

Le circuit RL parallèle est composé d'une résistance purement ohmique et d'une inductance (self, bobine, enroulement de moteur, etc.) pure. A noter qu'une inductance non pure se modélise avec un circuit RL série dont la résistance est celle du fil constituant la bobine. Pour plus de renseignements à ce sujet, revoir la théorie des inductances

Le circuit RL parallèle a une caractéristique globale pour laisser bloquer le courant qui se nomme impédance.

Principales caractéristiques de ce montage:
    - la tension est la même pour les trois éléments - R, X_l,Z
    - les courants sont différents:
        a) I_r est en phase avec U
        b) I_l est en retard de 90 degrés par rapport à U
        c) I_z - aussi tension d'alimentation - présente un décalage compris entre 0 et 90 degrés.
    - le circuit est dit inductif.

Le calcul de l'impédance de ce montage peut se faire soit en utilisant le rapport

Z = U_z/I_z   [W]

soit en utilisant Pythagore (voir graphique ci-dessus). Attention dans ce cas, il ne faut pas oublier que chaque côté représente l'inverse des grandeurs ohmiques: c'est à dire 1/R, 1/X et 1/Z. Il est souvent plus simple de calculer les courants dans la résistance et dans l'inductance, puis avec Pythagore I_z et finalement Z avec U_z/I_z.
Note: le cos f dans ce couplage = Z/R.

Pour le calcul des puissances active, apparente et réactive, il faut utiliser les formules suivantes :

note : puissance 0,5 => racine carré de

LES IMPÉDANCES

L'impédance permet d'exprimer les caractéristiques d'un récepteur. Ce dernier peut être composé d'un seul élément (p. ex. une résistance R, une inductance L ou d'un condensateur - défini par sa capacité C ) ou d'une combinaison de plusieurs de ces éléments couplés soit en série soit en parallèle, soit encore dans un couplage mixte.

L'unité de l'impédance s'exprime en ohm [W]. Sa caractéristique est non seulement de limiter la quantité de courant mais aussi d'indiquer le déphasage courant - tension (angle f). Dans un circuit alternatif, le cos f est également le facteur de puissance.

Pour calculer la valeur d'une impédance il faut :
- soit connaître la tension à ses bornes et le courant qui la traverse - l'on applique alors la loi d'ohm c'est à dire Z = U_z / I_z
- soit connaître la valeur et le couplage de chacun de ses constituants - l'on fait alors soit l'addition vectorielle (géométrique) des valeurs ohmiques de ces constituants dans le cas d'un couplage série,
- soit l'addition vectoriel (géométrique) de l'inverse des valeurs ohmiques de ces constituants dans le cas d'un couplage parallèle.

Pour déterminer l'angle f, on utilise les rapports trigonométriques sinus, cosinus, ou tangente :

- soit des valeurs ohmiques de ces constituants dans le cas d'un couplage série,

f = arcos (R/Z)
ou f = arcsin ((X_l-X_c)/Z)
ou f = arctg ((X_l-X_c)/R)

- soit de l'inverse de ces valeurs dans le cas d'un couplage parallèle.

f = arcos (Z/R)
ou f = arcsin ((1/X_c-1/X_l)*Z)
ou f = arctg ((1/X_l-1/X_c)*R)

Pour plus détails, voir les circuits RL, les circuits RC, les circuits RLC ou les filtres.

LES CIRCUITS RC

Dans les circuits RC nous allons voir d'abord le couplage RC série puis le couplage RC parallèle.
Le circuit RC série est composé d'une résistance (purement résistive) et d'une capacité (condensateur) pure. A noter qu'un condensateur non pur se modélise avec un circuit RC série . Pour plus de renseignements à ce sujet, revoir la théorie des condensateurs

Le circuit RC série a une caractéristique globale pour limiter le courant qui se nomme impédance.

Principales caractéristiques de ce montage:
    - le courant est le même pour les trois éléments - R, Xc,Z
    - les tensions sont différentes:
        a) U_r est en phase avec I
        b) U_c est en retard de 90 degrés par rapport à I
        c) U_z - aussi tension d'alimentation - présente un décalage compris entre 0 et 90 degrés.
    - le circuit est dit capacitif.

Le calcul de l'impédance de ce montage peut se faire soit en utilisant le rapport

Z = U_z/I_z

soit avec Pythagore Z =   ( R² + X_c² )^0,5

exercices RC série

LES CIRCUITS RC PARALLÈLE

Le circuit RC parallèle est composé d'une résistance purement ohmique et d'une capacité (condensateur) pur.

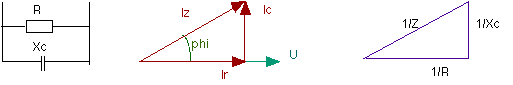
Le circuit RC parallèle a une caractéristique globale pour limiter le courant qui se nomme impédance.

Principales caractéristiques de ce montage:
    - la tension est la même pour les trois éléments - R, X_c,Z
    - les courants sont différents:
        a) I_r est en phase avec U
        b)Ic est en avance de 90 degrés par rapport àU
        c) I_z - aussi tension d'alimentation - présente un décalage compris entre 0 et 90 degrés.
    - le circuit est dit capacitif.

Le calcul de l'impédance de ce montage peut se faire soit en utilisant le rapport

Z = U_z/I_z  [W]

soit en utilisant Pythagore (voir graphique ci-dessus). Attention dans ce cas, il ne faut pas oublier que chaque côté représente l'inverse des grandeurs ohmiques: c'est à dire 1/R, 1/X et 1/Z. Il est souvent plus simple de calculer les courants dans la résistance et dans l'inductance, puis avec Pythagore I_z et finalement Z avec U_z/I_z.
Note: le cos f dans ce couplage = Z/R.

Pour le calcul des puissances active, apparente et réactive, il faut utiliser les mêmes règles quelque soit le couplage. :

P = U_r . I_r  [W]
Q = U_x . I_x    [VAr]
S = U_z . I_z    [VA]

LES PUISSANCES

voir les puissances en triphasé.

En monophasé

La puissance active exprime la puissance réellement utile (par exemple: puissance d'un chauffage, d'une lampe, d'un moteur - celle qui est convertie en puissance mécanique)

La puissance apparente est celle que doit fournir le distributeur pour alimenter l'ensemble des récepteurs. Elle est toujours plus grande que la puissance active sauf si Z égale R, alors S = P

La puissance réactive est une composante de la puissance apparente (l'autre étant la puissance active). Elle est décalée de 90 degrés par rapport à la puissance active. Elle exprime la puissance absorbée par des inductances pures ou des condensateurs. Cette puissance n'est pas utilisable dans la plupart des cas. Les distributeurs d'énergie en limite la quantité en imposant un facteur de puissance ( cos f ) minimum. On peut améliorer ce facteur en installant des condensateurs (par ex.:armature TL capacitive, batterie de compensation,...). cette puissance n'est pas utile ni dans les chauffages, ni dans les sources de lumière, ni dans les transformateurs d'énergie (moteurs).

Pour le calcul des puissances active, apparente et réactive, il faut utiliser les mêmes règles quelque soit le couplage. :

puissance active:    P = U_r . I_r = R . I_r²= U_r²/ R = S . cos f [W]
puissance réactive: Q = U_x . I_x =Z . I_x² = U_x² . X = S . sin f [var]
puissance active:    S = U_z . I_z = Z . I_z²= U_z² /Z = (P² + Q²)^0,5 [VA]

Dans un montage à plusieurs récepteurs on peut calculer les puissances ainsi:
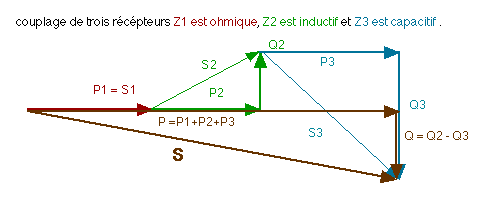- la puissance active = la somme arithmétique des puissances actives :

P = P₁+P₂+ ... +P_n
- la puissance réactive = la somme algébrique des puissances réactives :

Q = Q₁ +- Q₂ +- ..... +- Q_n
- la puissance apparente = la somme géométrique des puissances apparentes  : addition vectorielle ( utilisez dans ce cas Pythagore).