|
| |
Analyse fréquentielle des systèmes linéaires
Réponse fréquentielle
L’objectif de l’analyse fréquentielle est d’étudier le comportement et
la réponse d’un système linéaire à une sollicitation sinusoïdale. La réponse en
fréquence du système est l’étude du régime permanent.
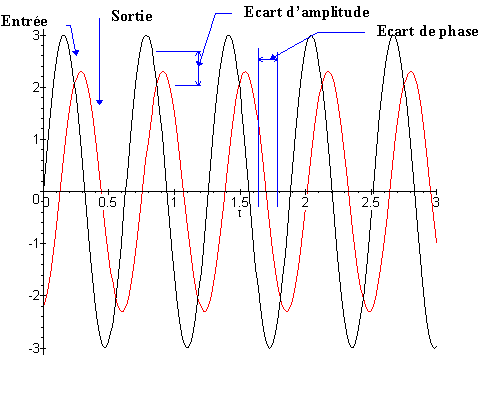
La sortie d’un système linéaire sollicité par un entrée sinusoïdale est de
forme sinusoïdale de même pulsation que le signal d’entrée mais d’amplitude
différente et déphasé par rapport au signal d’entrée.
Fonction de transfert complexe
Fonction de transfert
(rappel)
La fonction de transfert d'un système linéaire continu et invariant est une fonction
de la forme:
Ou E(p) et S(p) sont les transformées dans le domaine de Laplace des
fonctions temporelles e(t) et s(t).
| On appelle fonction de transfert complexe (ou transmittance
isochrone) la fonction obtenue en remplaçant la variable de Laplace (p) par le terme jw (imaginaire pur) |
La fonction de transfert complexe est donc:
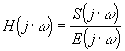
|
Lieux de transfert
La fonction 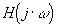 est une fonction complexe
de la variable w , l'étude de cette fonction peut se faire de
manière graphique. est une fonction complexe
de la variable w , l'étude de cette fonction peut se faire de
manière graphique.
On distingue principalement trois représentations graphiques
Les diagrammes de BODE, la représentation de NYQUIST, la représentation
de BLACK.
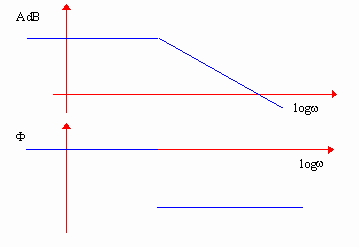
Diagrammes de BODE
Les diagrammes de Bode représentent séparément le module
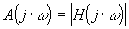 et la phase et la phase 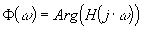 de la fonction de la fonction 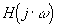 en
fonction de w , en
fonction de w ,
l’échelle horizontale est le log10 de la pulsation.
L’échelle pour le module est le dB
c’est à dire :
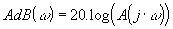
La phase est en général gradué en degré °. |
|
Cette représentation se prête bien à l'analyse des fonctions de transfert en effet,
si 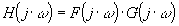 (Fonctions de transfert en série),
alors (Fonctions de transfert en série),
alors
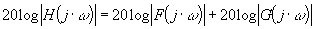
et
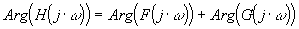
Il suffit donc d'ajouter les diagrammes des fonctions 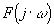 et et 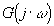 aussi bien sur
le diagramme d’amplitude que sur le diagramme des phases pour obtenir les diagrammes
de aussi bien sur
le diagramme d’amplitude que sur le diagramme des phases pour obtenir les diagrammes
de 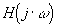 . .
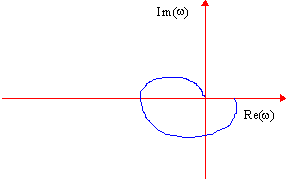
La représentation de NYQUIST
La représentation de Nyquist est la représentation dans
le plan complexe de la fonction 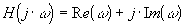 Le
graphique représentant la fonction de transfert doit être gradué dans le sens des w croissants. |
 |
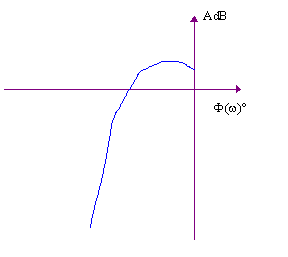
La représentation de BLACK.
C'est la représentation préférée des automaticiens,
c'est une représentation globale dans un système de coordonnées spécifiques. On
représente la phase 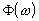 en degré en abscisse
et le module en degré en abscisse
et le module  en décibel. en décibel.La courbe
obtenue doit être gradué en pulsation.
Comme pour les diagrammes de Bode, la représentation d'un produit de fonction
s'obtient rapidement à partir des représentations de chacune des fonctions, ainsi une
multiplication par K revient à translater la courbe verticalement de 20 log (K).
attention : l’addition de courbe doit être réalisée pulsation par
pulsation |
 |
Système du premier ordre
Rappel
| On appelle système du premier ordre, tout système régit
par une équation différentielle linéaire à coefficients constant du premier ordre: 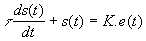
avec 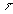 : constante de temps >0; : constante de temps >0;
K: gain statique |
on pose: 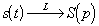
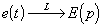 . .
En appliquant la transformation de Laplace à l'équation précédente, on obtient:
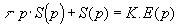
d'où la fonction de transfert:
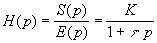
|
Représentation fréquentielle
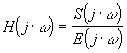 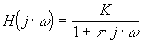
d'où le module et l'argument
Diagrammes de BODE. Diagrammes
Asymptotiques
Module
On représente le module (en dB) en fonction de w
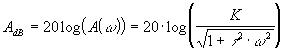
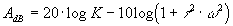
Etude des asymptotes
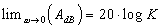 asymptote horizontale asymptote horizontale
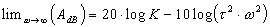
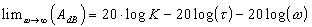
Dans le système de cordonnées du diagramme de Bode, l'asymptote est une droite
d'équation. 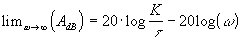
On dit que la pente est de -20dB par décade (le module diminue de 20dB pour une
augmentation d'un facteur 10 de w ).
Les deux asymptotes se croisent pour 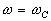 ,
cette fréquence est appelée fréquence de cassure. ,
cette fréquence est appelée fréquence de cassure.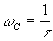
| Diagramme de BODE (amplitude) 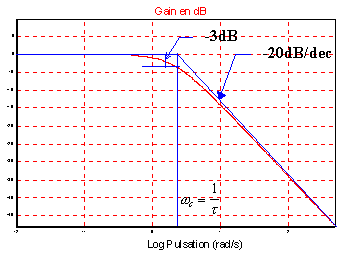
|
Le diagramme asymptotique est suffisamment précis pour
être utilisé tel quel. Ecart par rapport aux asymptotes pour quelques points.
pour 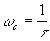 : : 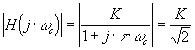
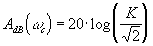
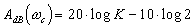
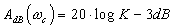
pour la fréquence de cassure l'écart par rapport à l'asymptote est de -3dB.
Pour les fréquences double et moitié, l'écart est de -1dB. |
| Diagramme de Bode (phase) 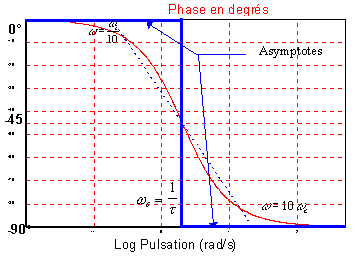
|
Le diagramme asymptotique à la forme d'une marche
d'escalier, il n'est pas suffisamment précis pour représenter l'évolution de la phase. Quelques
points:
fréquence de cassure 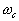
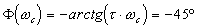
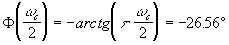
 On peut tracer la droite passant par
les points On peut tracer la droite passant par
les points 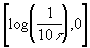 et et 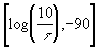 pour faciliter le tracé (attention ce n'est pas une tangente). pour faciliter le tracé (attention ce n'est pas une tangente).
|
La représentation de NYQUIST
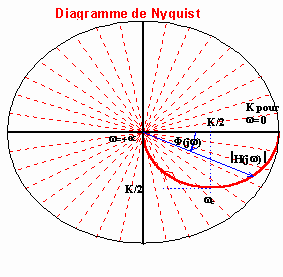 |
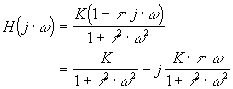 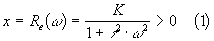
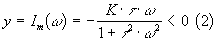
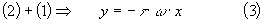
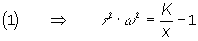
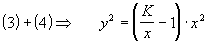
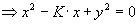
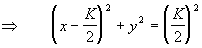
Le lieu de Nyquist d'un système du premier ordre est un demi cercle de centre [0,K/2]
et de rayon K/2.
pour  w =0,
le déphasage est nul. w =0,
le déphasage est nul.
Pour w ® µ
, (haute fréquence) le gain tend vers 0 et la phase vers 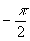 (vers le point [0,0]. (vers le point [0,0]. |
La pulsation de cassure  correspond au point correspond au point 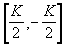 . .Le
lieu doit être gradué en w croissant. pour être utilisable.
On peut passer rapidement des diagrammes de Bode au lieu de Nyquist en reportant pour
chaque pulsation le module et la phase. |
Représentation de BLACK.
Système du second ordre
Rappel
| On appelle système du second ordre tout
système régit par une équation différentielle linéaire à coefficients constant du
second ordre. 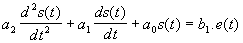
soit sous la forme canonique
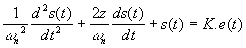
avec 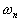 : Pulsation propre du système non
amorti : Pulsation propre du système non
amorti
 gain statique gain statique
z (ou x ou m) facteur d'amortissement
|
Fonction de transfert:
Dans les conditions d'Heaviside (s(0)=0, s'(0)=0).
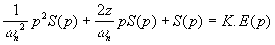 donc donc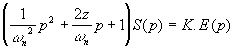
donc la fonction de transfert est:
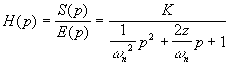
En fonction de la valeur de z, la forme temporelle sera différente (Cf.
représentation temporelle)
0<z<1 réponse temporelle oscillatoire amortie
z=1 réponse temporelle apériodique critique
z>1 réponse apériodique
|
Représentation fréquentielle
Fonction de transfert isochrone
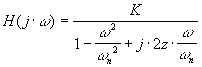
Module
|
Argument
|
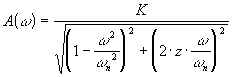
|
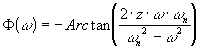
|
Diagrammes de BODE
Allure générale des courbes d’amplitude
| Diagramme de Bode (amplitude) 
|
On voit sur les diagrammes ci-contre que l'évolution du
module est fonction de la valeur de z: on retrouve pour tous les tracés un asymptote
horizontale lorsque
w ® 0 (20 log K) et un asymptote de
-40dB par décade lorsque
w ® µ
(droite d'équation 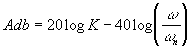 ) )
Les deux droites se coupent pour 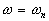
En fonction de z certaines courbes présentent un maximum.
|
Résonance - coefficient de surtension
On pose 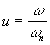 (pulsation réduite), on a
donc: (pulsation réduite), on a
donc: 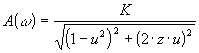 , cette fonction présente un
maximum. , cette fonction présente un
maximum.
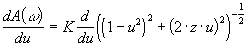
donc 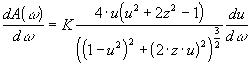 , ,
La dérivée s'annule 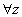 pour pour 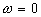 (asymptote horizontale) mais aussi pour (asymptote horizontale) mais aussi pour 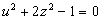 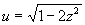 si si 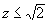
La pulsation correspondante est appelée pulsation de résonance : 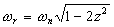
On définit le coefficient de surtension 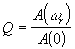
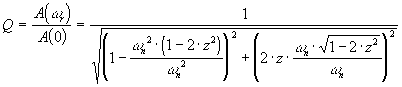
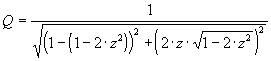 donc : donc : pour pour 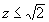 . .
La surtension n’existe que si le coefficient d’amortissement est inférieur
à  . On définit en général la valeur en
dB de la surtension, . On définit en général la valeur en
dB de la surtension,  . Une valeur usuelle
de réglage d’un asservissement est QdB=2,3dB. . Une valeur usuelle
de réglage d’un asservissement est QdB=2,3dB.
Etude complète pour z<1
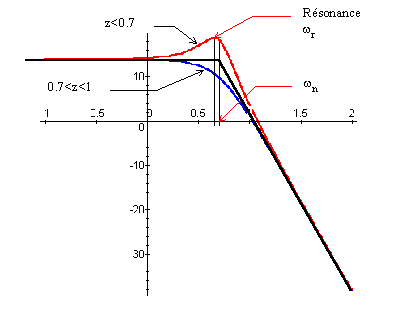
Diagramme d’amplitude
| 
|
Un système du second ordre avec z<1 est parfaitement
défini par le tracé de ces asymptote Il peut être nécessaire de compléter le tracé
par la pulsation de résonance et l'amplitude correspondante.
Pour z<0,7 on a la courbe est toujours au-dessus des asymptotes et le système
possède une résonance :
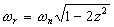
le coefficient de surtension s’écrit :
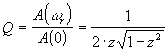
pour 1>z>0.7, le diagramme reste sous les asymptotes (pas de surtension).
|
Diagramme des phases
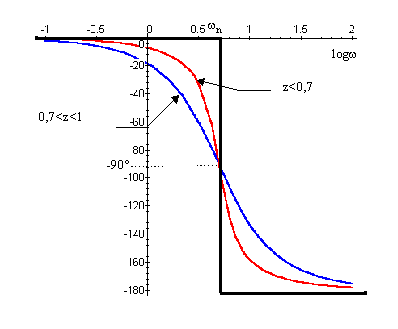 |
Le diagramme asymptotique est composé de 2 droites
horizontales: 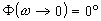 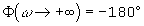
Le changement de phase à lieu pour la pulsation de cassure.
Le diagramme asymptotique est assez proche de la courbe réelle.
Remarque : plus z est grand plus la courbe est écartée des asymptotes. |
Etude pour z>1
| H(p) la fonction de transfert d'un système du second ordre
avez z>1 Dans ce cas il est préférable d’étudier le système comme le
produit de deux systèmes du premier ordre
|
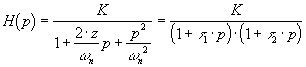 donc donc 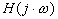 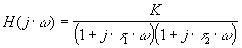
|
Diagramme d’amplitude
Diagramme des phases
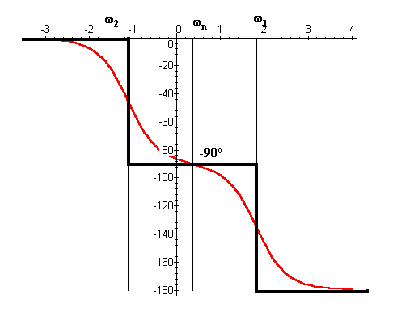 |
Le diagramme asymptotique relatif à la phase présente
deux décrochements :
le premier pour 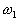 introduit un changement
de phase de-90° ; introduit un changement
de phase de-90° ;
le deuxième pour 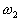 un nouveau
décrochement de -90° ; un nouveau
décrochement de -90° ;l'asymptote à l'infini est de -180°.
|
Représentation de NYQUIST
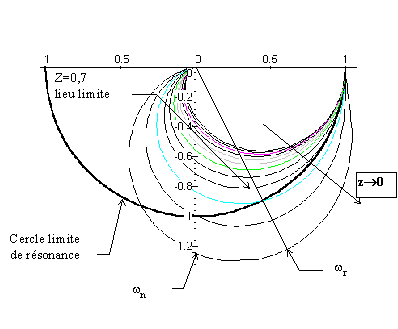 |
Pour w =0 le module Adb(0)=K, (le
tracé ci-contre est pour K=1)
pour w =+µ , le module =0 et
l'argument tend vers -180°
si 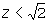 la courbe passe au delà du cercle
de rayon K, la pulsation de résonance est obtenue pour le module maximal. la courbe passe au delà du cercle
de rayon K, la pulsation de résonance est obtenue pour le module maximal.
La pulsation de résonance se mesure à l’intersection avec l’axe imaginaire.
La tangente pour w =+µ , est de
-180°. La courbe ne passe pas au dessus de l’axe réel.
|
Représentation de BLACK.
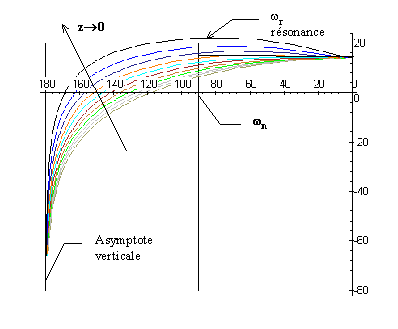 |
Le diagramme ci-contre représente différents tracés en
fonction de z de système de 2nd ordre, L'asymptote verticale est pour
F =-180° |
Synthèse
On peut donc, a partir de la réponse impulsionnelle et de la réponse fréquentielle,
définir plusieurs pulsations caractéristiques pour les systèmes du second ordre.
Autres formes particulières
Premier ordre généralisé
Un premier ordre généralisé est de la forme  . .
Etudier la représentation fréquentielle de ce système (Cf. Travaux dirigés)
Premier ordre avec intégration
Etudier la fonction de transfert suivante :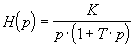 , ,
Représentation fréquentielle ? (Cf. Travaux dirigés)
Second ordre avec intégration
Etudier la fonction de transfert suivante :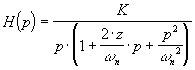 , ,
Représentation fréquentielle ? (Cf. Travaux dirigés)
Tracés asymptotiques d'une
fonction de transfert quelconque
Forme générale
Toute fonction de transfert d'un système peut se mettre sous la forme :
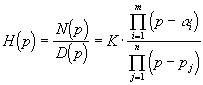 |
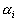 : zéro de
H(p) : zéro de
H(p)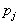 : pôles de H(p) : pôles de H(p)
n: ordre de H(p) |
Cette expression peut aussi se mette sous la forme
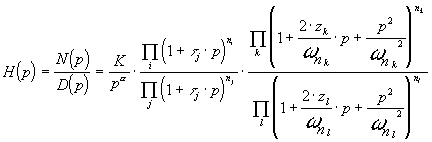 |
c'est à dire en faisant apparaître des formes types du
premier et de second ordre avec
a : classe de H(p) |
Une fonction de transfert quelconque est donc le produit de fonctions élémentaires
| Constante |
Fonction puissance |
Fonction du premier ordre |
Fonction de second ordre |
| K |
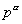 |
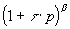 |
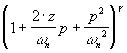 |
|
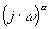 |
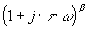 |
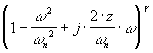 |
avec a , b , g
, entiers relatifs.
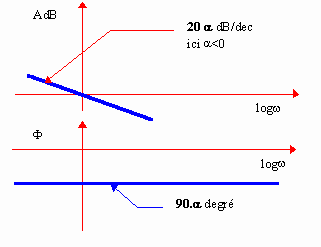
Terme 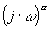
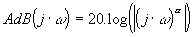 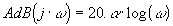
soit une droite de pente 20.a dB par décade
remarque si a =0, asymptote horizontale.
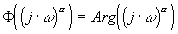
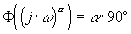
soit une droite horizontale |
 |
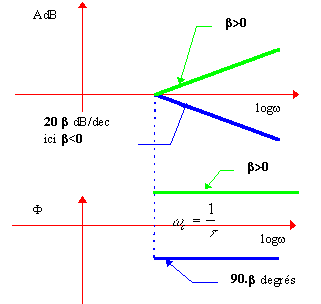
Terme 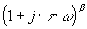
le terme 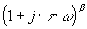 amène à partir de la valeur
amène à partir de la valeur 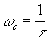 une droite
de pente 20.b dB par décade. une droite
de pente 20.b dB par décade.on retrouve pour .b =-1 un système du premier ordre.
la phase est décalée à partir de cette même valeur de -.b
.90°
|
 |
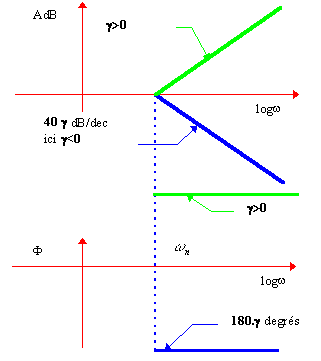
Terme 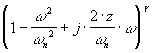
Le terme 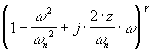 amène un changement de pente de 40.g dB/décade à partir de
la pulsation de cassure
amène un changement de pente de 40.g dB/décade à partir de
la pulsation de cassure 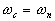 et un déphase de et un déphase de
g *.180°. |
 |
|