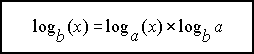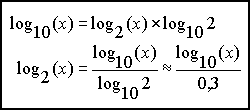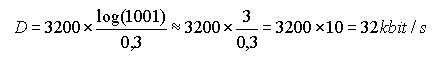Codage
|
Généralités
su le codage
|
|
Ce
mot est utilisé de manière très diverse (souvent
à contresens).
Dans la littérature technique il englobe indifféremment
toutes les méthodes de compression, les paramètres d'échantillonnage
et la résolution...
Cet hiatus persiste pour les logiciels ou matériels procédant
à la compression des sons et vidéos qui sont appelés
des codecs et dont la traduction est tantôt "codeurs
- décodeurs", tantôt "compresseurs
- déccompresseurs)
En
principe, le codage désigne le type de correspondance que l'on
souhaite établir entre chaque valeur du signal analogique et
le nombre binaire qui représentera cette valeur.
Bien
entendu, la résolution du convertisseur est un élément
du codage.
Plus on attribue de bits à chaque échantillon, plus la
restitution sera fine, mais plus le volume de mémorisation ou
le temps de transmission sera élevé, plus débit
en ligne de transmisssion sera grand.
Par
exemple, pour le son téléphonique, les américains
ont opté un codage sur 7 bits , les européens sur 8. La
vitesse d'échantillonnage étant fixée à
8 000 échantillons par seconde, le flux numérique américain
pour la parole téléphonique s'établit à
56 k bit/s, alors que l'Europe a adopté 64 k bit/s - bande d'un
canal RNIS par exemple.
Les
standards d'enregistrement sonore pour CD-ROM codent sur 16 bits, ce
qui leur permet de différencier 65 635 échelons d'intensité
sonore.
Un
deuxième élément important est le type de codage
: PCM - Différentiel (delta) - Prédictif - Adaptatif -
etc. - c.f. ci-dessous
|
Codage PCM
Codage PCM
PCM : Pulse
Coded Modulation - En français : MIC Modulation par
Impulsions Codées
Lorsque
la taille de l'enregistrement numérique n'est pas un critère
important, on peut se permettre de coder chaque échantillon à
sa valeur réelle (contrairement à ce qui se fait dans
le codage différentiel p. ex.).
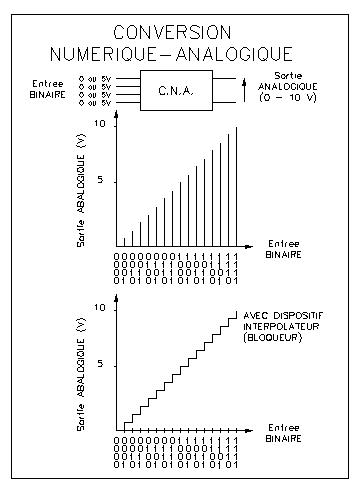
C'est
ce que nous avons fait dans les figures ci-dessus : "Conversion
Analogique-Numérique", "Conversion Numérique-Analogique",
et "Reconversion d'un signal numérique en signal analogique".
|
|
M
Ne
R
Fe
D
O
|
Nombre d'octets occupés
en mémoire
Nombre total d'échantillons
Résolution du convertisseur ( bit )
Fréquence d'échantillonnage (bit/s)
Durée d'enregistrement (s)
Débit binaire en octets par seconde |
|
M = Ne.(R/8) = (D.Fe).(R/8)
|
|
O = M/D = Fe.(R/8)
|
|
Bande passante en bit/s : Fe.R
|
|
Valeurs usuelles pour le
codage MIC
Modulation par Impulsions Codées
PCM (Pulse Coded Modulation)
|
|
Echantillons/s
( Hz )
|
Résolution
( bits )
|
Mono
Stéréo
|
Débit
( octets/s)
|
|
8000
|
8
|
Mono
|
8 000
|
|
8000
|
8
|
Stéréo
|
16 000
|
|
8000
|
16
|
Mono
|
16 000
|
|
8000
|
16
|
Stéréo
|
32 000
|
|
11 025
|
8
|
Mono
|
11 025
|
|
11 025
|
8
|
Stéréo
|
22 050
|
|
11 025
|
16
|
Mono
|
22 050
|
|
11 025
|
16
|
Stéréo
|
44 100
|
|
22 050
|
8
|
Mono
|
22 050
|
|
22 050
|
8
|
Stéréo
|
44 100
|
|
22 050
|
16
|
Mono
|
44 100
|
|
22 050
|
16
|
Stéréo
|
88 200
|
|
44 100
|
8
|
Mono
|
44 100
|
|
44 100
|
8
|
Stéréo
|
88 200
|
|
44 100
|
16
|
Mono
|
88 200
|
|
44 100
|
16
|
Stéréo
|
176 400
|
Codage différentiel ou codage "delta"
|
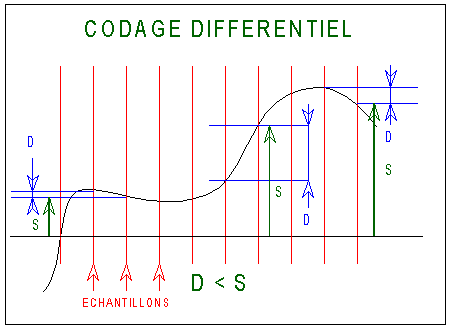
Le
codage différentiel ou codage delta
évalue la différence entre le niveau du signal
à l'instant de l'échantillonnage
et le niveau qu'il avait lors de l'échantillonnage précédent.
|
|
|
|
On observe
en effet que la voix présente rarement des fortes transitions
de niveau entre deux échantillonages successifs.
La différence à coder est généralement moins
grande que le signal lui-même.
Le nombre de bits de codage peut être diminué. Ce qui réduit
l'occupation en mémoire ou la bande passante (en bit/s) occupée
lors d'une transmission, ou lle temps de transfert dans une page Internet.
Bien entendu,
si une transition brutale dépasse l'étendue maximale du
codage, un écrêtage ponctuel se produira. Si ce fait est
rare et que l'exigence de qualité de l'application est basse,
ce codage permet de réduire dans de grandes proportions la bande
passante attribuée au signal : transmission plus rapide, espace
mémoire plus réduit, stockage ou transmission plus économiques.
Comme une
dérive importante peut avoir lieu après de nombreux calculs
de différence, la valeur exacte d'un échantillon est transmise
à des moments régulièrement espacés.
|
|
M
Ne
C
Fe
D
O
|
Nombre d'octets occupés
en mémoire
Nombre total d'échantillons
Nombre de bits de codage ( bit )
Fréquence d'échantillonnage (bit/s)
Durée d'enregistrement (s)
Débit binaire en octets par seconde |
|
M = Ne.(R/8) = (D.Fe).(C/8)
|
|
O = M/D = Fe.(C/8)
|
|
Bande passante en bit/s : Fe.C
|
On obtient des formules
analogues au codage PCM où la résolution R du convertisseur
est remplacée par le nombre de bits de codage C. Comme en codage
différentiel les quantités à coder sont plus faibles,
on peut se permettre de les coder en moins de bits, ce qui réduit
à la fois l'occupation en mémoire, le débit binaire
et la bande passante en transmission temps réel.
Le codage prédictif
est basé sur la même constatation.
Il prévoit la valeur suivante d'après l'historique des valeurs
échantillonnées passées.
Le codage mesure seulement la différence entre la valeur prédite
et la valeur réelle.
Si la loi de prédiction est bonne, le codage mesure des valeurs
voisines de zéro. |
Le codage est dit
adaptatif lorsqu'il adapte le nombre de bits au type de
variation sonore qu'il détecte.
Il est très utile pour adapter la qualité d'un son à
l'encombrement du réseau qui le transmet. |
Capacité d'un canal numérique bruité -
Bande passante d'un signal numérique
Une formule
précise la bande passante maximale pour un signal numérique
traversant une ligne réelle donc bruitée.
Elle comporte deux
aspects, elle permet de calculer :
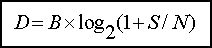
D : débit
binaire maximal (bit/s)
B : bande passante (Hz)
S/N : rapport Signal/Bruit (W/W)
On remarquera que le logarithme utilisé est en base 2
Traitement
Numérique du Signal - M Bellanger - ED. Masson
- p 58
La bande
passante que doit avoir un canal pour écouler convenablement un signal
numérique est générament plus élevée que
celle nécessaire pour le signal analogique initial (supposé
occuper une bande limitée).
Calculons
le débit binaire maximum pour une ligne téléphonique analogique banale limitée
à la bande réservée aux conversations téléphoniques (dite POTS).
On admettra un rapport S/B de 30 dB.
Les lignes
téléphoniques ont ne bande passante maximale de 0 à 4
kHz, (en pratique on se limite à 300 Hz - 3,5 kHz, donc une bande passantede
B = 3 200 Hz).
Calcul
approximatif :
30 dB correspond à un rapport de puisances de 1000 : voir notre rubrique
"Décibels"
1 + S/N = 1001 # 1024 ; or, 2 puissance 10 = 1024 ; donc D = 3200 . 10 = 32
kbit/s
Pour la bande passante théorique de 4 kHz on obtiendrait 40 kbit/s
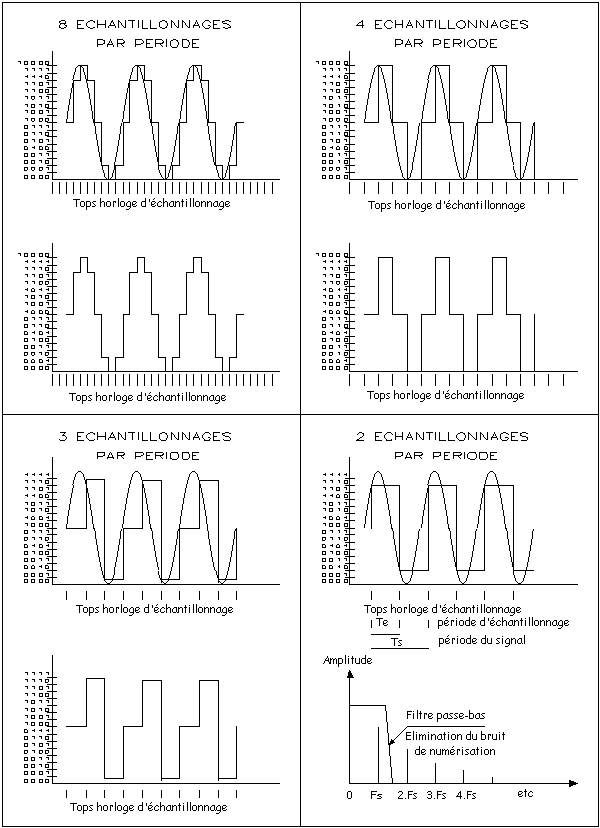
Or, d'après le théorème de l'échantillonnage (c.f.
ci-dessus) celui-ci doit se faire à 8 kbit/s.
Comme le codage se fait généralement sur 8 bits, c'est un débit
de 64 kbit/s qui serait nécessaire.
Conclusion : le son téléphonique numérisé
ne pourrait pas franchir la boucle terminale d'abonné sans être
préalablement compressé.
Pour le calcul
sans approximatiopns il faut s"appuyer sur la formule :
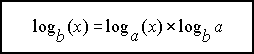
avec a
= 2 et b = 10 :
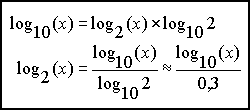
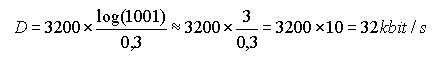
Compression
Un son numérisé
est une séquence d'octets en mémoire.
La compression consiste à trouver une séquence d'octets
plus courte dont l'effet sonore soit semblable à celui de la séquence
initiale.
Buts
de la compression :
Codecs
La compression
est onbtenue grâce à des algorithmes complexes et variés
mis en oeuvre dans de nombreux programmes appelés codecs disponibles
dans le commerce.
Si l'on fait son choix parmi les codecs les plus performants, les seuls qui
subsistent, plus on compresse, plus la qualité du son final se dégrade.C'est
pourquoi chacun d'eux correspond à une application particulière.On
distingue entre autre, trois qualités principales de son :
-
qualité
téléphone
-
qualité
radio
-
qualité
CD
Mais les
codecs disponibles permettent toute une gamme de qualités intermédiaires
en vous donnant le choix de combiner divers modes de compression, diverses
fréquences d'échantillonnage et diverses résulutions.
Voir "Standards
de numérisation du son"
Voir également sur la toile : http://www.terran-int.com/CodecCentral/Codecs/index.html