
Le son est une variation rapide de la pression atmosphérique.
Pour son traitement, il est généralement transformé en
variations proportionnelles de tension électrique grâce à
des dispositifs appelés d'une manière générale "microphones".

Le son donne lieu à des traitements divers :
Pour comprendre ces techniques de traitement, il est indispensable de connaître les caractéristiques mathématiques de base des fonctions qui représentent les ondes sonores
Les titres qui vont suivre se rapportent aux deux approches des sons : mathématique et musicale.
C'est ce que l'on nomme généralement la "force"
d'un son. Fort, faible, "fortissimo"ou "pianissimo" etc.
Les théoriciens de la musique parlent de forte ou faible sonie.
Cela correspond physiquement à l'amplitude des variations
de pression de l'air.
Ou celle de la tension généréepar le picrophone.
Comme tout phénomène impliquant la physiologie, la sonie se repère en décibels.
Il est indispensable de se familiariser
avec ce mode de repérage,
décrit à la rubrique "Décibels" : ![]()
Musicalement, on parle d'un son aigu ou grave. Les théoriciens
de la musique parlent de "tonie" ékevée ou basse.
Physiquement, cela correspond à la fréquence - nombre de
variations de pression par seconde (Hertz, Hz).
Plus un son est aigu, plus sa fréquence est élevée.
|
La bande des fréquences audibles par les êtres
humains s'étale entre
quelques dizaines de Hertz à 16 kHz ou 20 kHz selon l'âge. |
Deux instruments différents ou deux personnes peuvent émettre un son de mêmes amplitude et fréquence et pourtant être reconnaissables. Ce ne sont pas exactement les mêmes sons. Qu'est-ce qui diffère ?
Les musiciens parlent de différences de timbre permettant de reconnaître les instruments
En réalité un son est rarement purement sinusoïdal.
Nous rappelons ci-dessous la définition d'une sinusoïde et ses grandeurs
caractéristiques :
amplitude A, fréquence F.
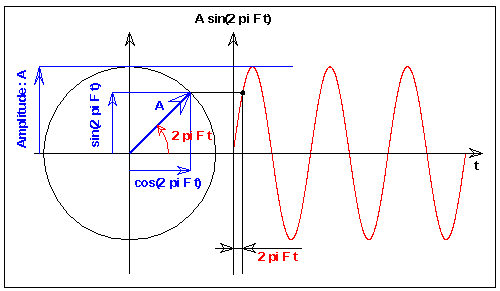
.
Le son est produit dans la grande majorité des cas par
des objets entrés en vibration de diverses manières.
Or, les lois de la physique impliquent que ces vibrations ne se font pas au
hasard : leurs dimensions jouent un grand rôle. D'unemanière générale,
plus les objets sont petits plus leur fréquence de vibration propre est
élevée et plus ils rendent un son aigu.
On a dessiné ci-dessous les déformations multiples
et simultanées que subit une lame ou une corde d'instrument vibrant librement
après un choc.
On peut les voir à l'aide d'un stroboscope elles ont généralement
une amplitude d'une fraction de millimètre à quelques millimètres..
Dans la figure ci-dessous, l'amplitude a été exagérée
pour les rendre pus visibles.
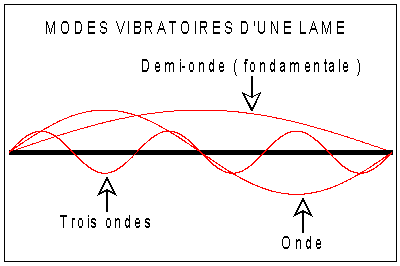
On observe plusieurs modes simultanés de vibration génèrant
des sinusoides dont les fréquences sont multiples de la plus basse d'entre
elles appelée vibration la fondamentale
Les autres vibrations ont naturellement pour fréquences celle de
la fondamentale multipliée par 2, 3 etc.
Ce sont les harmoniques 2, 3 etc.
|
|
Cette observation expérimentale, que les facteurs d'instruments de musique mettent si bien à profit pour enrichir la gamme harmonique de leurs créations, fait l'objet d'un théorème de mathématiques qui s'énonce :
- Théorème de Fourier -
| Toute fonction périodique de fréquence F peut être décomposée en une somme de fonctions sinusoïdales de fréquences 2F, 3F, ... multiples entiers de F. |
Pour des sons naturels, les amplitudes des harmoniques décroissent rapidement quand leur rang augmente.

Les harmoniques de rang élevé ont donc généralement
peu d'influence sur la qualité du son.
Comme, de plus, elles sont généralement techniquement difficiles
à gérer, l'ensemble des techniques liées au traitement
du son ne considèrent que celles qui se trouvent dans la bande audible.
Il en est de même pour les fréquences très basses, inaudibles.
Par exemple, dans les techniques de transmission téléphonique
de la voix, on ne traite théoriquement que les fréquences situées
entre 0 Hz et 4 kHz. Pratiquement entre 300 Hz et 3 kHz. Cela suffit pour une
bonne reproduction de la voix qui reste très reconnaissanble.
En contrepartie l'économie faite sur les équipements ainsi que
la possibilité de gérer de très multiples communications
sur des lignes communes (multiplexage) sont des avantages considérables.
En revanche, les équipements sonores de qualité traitent les harmoniques dans la bande des 50 Hz à 16 kHz, voire 20 kHz.

| Retour au carrefour précédent "Physique et représentation des données" | |
| Retour au carrefour "Réseaux" |