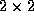 symétrique, de longueur
L est :
symétrique, de longueur
L est :




Le comportement d'un coupleur est bien décrit par sa matrice
de transfert, c'est-à-dire la matrice qui relie les amplitudes modales
des guides de sortie à celles des guides d'entrée du coupleur.
Par exemple, la matrice de transfert d'un coupleur 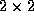 symétrique, de longueur
L est :
symétrique, de longueur
L est :
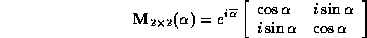
avec

et
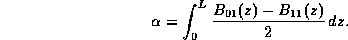
Ici 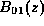 et
et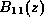 sont les constantes de propagation du supermode fondamental local LP
sont les constantes de propagation du supermode fondamental local LP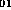 et du premier supermode antisymétrique LP
et du premier supermode antisymétrique LP .
Les limites du coupleur, z=0 et z=L, sont définies
par les points à partir des quels les guides individuels peuvent
être considérés comme indépendants. Le paramètre
.
Les limites du coupleur, z=0 et z=L, sont définies
par les points à partir des quels les guides individuels peuvent
être considérés comme indépendants. Le paramètre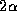 est donc le déphasage accumulé par ces deux supermodes le
long du coupleur.
est donc le déphasage accumulé par ces deux supermodes le
long du coupleur.
A partir de la matrice de transfert, on peut, pour une excitation donnée correspondant à un vecteur colonne donné, calculer la puissance transmise dans chaque branche. Par exemple, une excitation dans la branche 1 correspond au vecteur d'entrée

et par conséquent une transmission (en intensité) dans la même branche
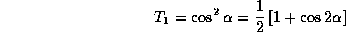
Lorsque les modes arrivent en phase (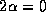 )
à z=L, la transmission est maximum dans la branche principale
(
)
à z=L, la transmission est maximum dans la branche principale
(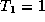 ). Lorsqu'ils arrivent hors
de phase (
). Lorsqu'ils arrivent hors
de phase (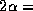 ¼)à
z=L, la transmission est minimum (
¼)à
z=L, la transmission est minimum (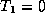 ),
correspondant à un transfert complet de puissance dans la branche
secondaire. A titre d'exemple, cet échange de puissance est montré
pour un coupleur très fusionné sur la figure 5.2
en fonction de l'élongation et sur la figure 5.3
en fonction de la longueur d'onde. Les figures 5.4
et 5.5 illustrent ces échanges
de puissances pour un coupleur très peu fusionné.
),
correspondant à un transfert complet de puissance dans la branche
secondaire. A titre d'exemple, cet échange de puissance est montré
pour un coupleur très fusionné sur la figure 5.2
en fonction de l'élongation et sur la figure 5.3
en fonction de la longueur d'onde. Les figures 5.4
et 5.5 illustrent ces échanges
de puissances pour un coupleur très peu fusionné.
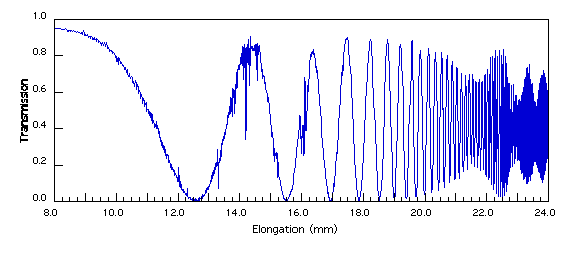
Figure 5.2: Enregistrement de la transmission dans la branche
principale d'un coupleur 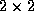 très fusionné en fonction de l'élongation. La transmission
dans la branche secondaire, aux pertes près, est le complément.
très fusionné en fonction de l'élongation. La transmission
dans la branche secondaire, aux pertes près, est le complément.
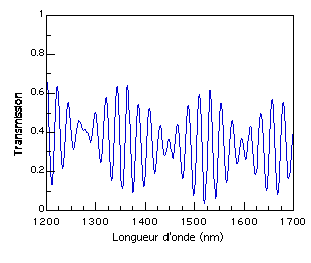
Figure 5.3: Enregistrement de la réponse spectrale du
coupleur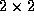 de la figure précédente
après 64 cycles de transfert de puissance.
de la figure précédente
après 64 cycles de transfert de puissance.
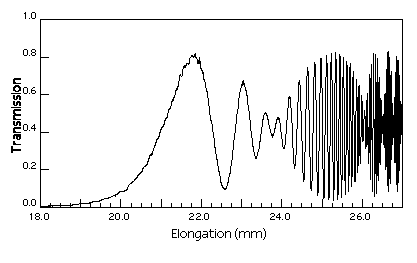
Figure 5.4: Enregistrement de la transmission dans la branche
principale d'un coupleur  peu fusionné en fonction de l'élongation. La transmission
dans la branche secondaire, aux pertes près, est le complément.
peu fusionné en fonction de l'élongation. La transmission
dans la branche secondaire, aux pertes près, est le complément.
Figure 5.5: Enregistrement de la réponse spectrale du
coupleur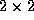 de la figure précédente
après 64 cycles de transfert de puissance.
de la figure précédente
après 64 cycles de transfert de puissance.
A partir des matrices de transfert, on calcule aussi aisément
les transmissions de coupleurs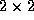 mis en série dans une structure d'interféromètre Mach-Zehnder
tout-fibre, telle qu'illustrée dans la section 6.1.
Il s'agit donc d'un formalisme fécond pour l'analyse de structures
à base de coupleurs
mis en série dans une structure d'interféromètre Mach-Zehnder
tout-fibre, telle qu'illustrée dans la section 6.1.
Il s'agit donc d'un formalisme fécond pour l'analyse de structures
à base de coupleurs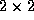 ;
en outre, il est généralisable aux autres coupleurs étoile
[14].
;
en outre, il est généralisable aux autres coupleurs étoile
[14].
Le déphasage accumulé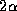 ,
comme pour les fibres effilées, dépend de l'allongement,
de la longueur d'onde, et de l'indice de réfraction du milieu extérieur;
il en résulte que la transmission d'un coupleur oscille en fonction
de ces paramètres. La réponse d'un coupleur donné
dépend non seulement du profil longitudinal déterminé
par le processus d'allongement, mais aussi du degré de fusion. Les
programmes développés pour calculer les supermodes scalaires
et les corrections de polarisation qui y sont attachées prennent
en compte les paramètres de fabrication [15].
Les réponses expérimentales telles que celles montrées
sur les figures 5.2, 5.3,
5.4 et 5.5
ont été reproduites par simulation pour différents
paramètres de fabrication [16],
validant ainsi les étapes du calcul théorique. Ces programmes
constituent de surcrot un excellent outil de design pour la conception
d'un coupleur ayant une réponse particulière.
,
comme pour les fibres effilées, dépend de l'allongement,
de la longueur d'onde, et de l'indice de réfraction du milieu extérieur;
il en résulte que la transmission d'un coupleur oscille en fonction
de ces paramètres. La réponse d'un coupleur donné
dépend non seulement du profil longitudinal déterminé
par le processus d'allongement, mais aussi du degré de fusion. Les
programmes développés pour calculer les supermodes scalaires
et les corrections de polarisation qui y sont attachées prennent
en compte les paramètres de fabrication [15].
Les réponses expérimentales telles que celles montrées
sur les figures 5.2, 5.3,
5.4 et 5.5
ont été reproduites par simulation pour différents
paramètres de fabrication [16],
validant ainsi les étapes du calcul théorique. Ces programmes
constituent de surcrot un excellent outil de design pour la conception
d'un coupleur ayant une réponse particulière.



