





Si l'on cherche un mode, c'est-à dire une solution du type

on doit résoudre l'équation de Helmholtz
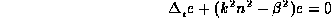
où k est le nombre d'onde dans le vide lié
à la longueur d'onde  par
par 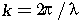 ,
, 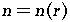 est une constante dans chacune des couches et
est une constante dans chacune des couches et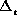 le laplacien transverse qui s'identifie à
le laplacien transverse qui s'identifie à
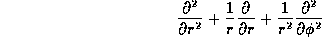
en coordonnées cylindriques. De plus, on cherche les solutions telles que la partie transversale du mode se sépare en partie radiale et partie azimutale selon :
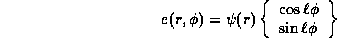
avec 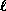 un entier
positif ou nul qui donne le nombre de zéros azimutaux du champ :
ainsi, lorsque
un entier
positif ou nul qui donne le nombre de zéros azimutaux du champ :
ainsi, lorsque 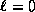 , les modes
n'ont pas de dépendance azimutale et sont donc à symétrie
circulaire. D'une façon générale, on doit résoudre
, les modes
n'ont pas de dépendance azimutale et sont donc à symétrie
circulaire. D'une façon générale, on doit résoudre
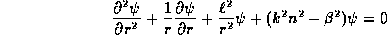
une équation différentielle de Bessel si 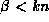 ou de Bessel modifiée si
ou de Bessel modifiée si 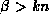 .
.
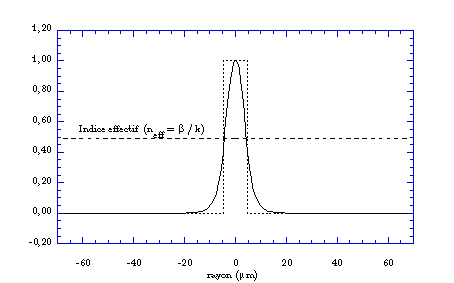
Figure 2.3: Profil du mode fondamental d'une fibre unimodale
comparé au profil d'indice du guide tous deux normalisés.
Supposons maintenant que la fibre est constituée de deux couches
: le coeur d'indice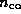 et de rayon
et de rayon 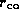 et la gaine optique d'indice
et la gaine optique d'indice 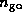 et de rayon infini. Avec les conditions aux limites à l'infini (
et de rayon infini. Avec les conditions aux limites à l'infini ( )
et à l'interface coeur-gaine (en
)
et à l'interface coeur-gaine (en 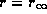 ),
on trouve les solutions pour un mode guidé :
),
on trouve les solutions pour un mode guidé :
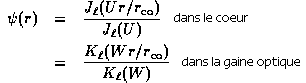
où 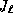 est une fonction
de Bessel et
est une fonction
de Bessel et 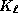 une fonction
de Bessel modifiée dordre
une fonction
de Bessel modifiée dordre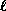 ;
U
et
W sont des paramètres modaux liés à la constante
de propagation
;
U
et
W sont des paramètres modaux liés à la constante
de propagation 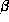 et définis
par
et définis
par
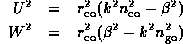
de telle sorte que
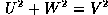
avec

qui définit V le paramètre du guide ou fréquence normalisée. La valeur de V détermine le régime d'opération.
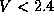 , un seul mode peut de
propager : c'est ce qu'on appelle le mode fondamental. On opère
dans le régime unimodal de la fibre. On dit aussi qu'elle est unimodale.
Dans ce cas
, un seul mode peut de
propager : c'est ce qu'on appelle le mode fondamental. On opère
dans le régime unimodal de la fibre. On dit aussi qu'elle est unimodale.
Dans ce cas 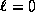 et le profil
du mode fondamental ressemble à une gaussienne ainsi que l'illustre
la figure 2.3.
et le profil
du mode fondamental ressemble à une gaussienne ainsi que l'illustre
la figure 2.3.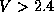 plusieurs modes peuvent
de propager. La fibre est multimodale.
plusieurs modes peuvent
de propager. La fibre est multimodale.Il est à noter que le paramètre V dépend
non seulement des données de la fibre ( et rayon du coeur
et rayon du coeur 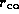 ), mais
aussi de k et donc de la longueur d'onde d'opération
), mais
aussi de k et donc de la longueur d'onde d'opération 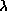 .
A titre d'exemple, pour un saut d'indice
.
A titre d'exemple, pour un saut d'indice 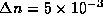 avec
avec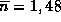 (silice dopée et
silice pure), le régime est unimodal (c'est-à-dire V<2,4)
(silice dopée et
silice pure), le régime est unimodal (c'est-à-dire V<2,4)
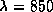 nm si
nm si 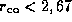
 m,
m,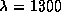 nm si
nm si 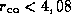
 m,
m,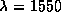 nm si
nm si 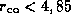
 m.
m.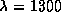 nm, devient multimodale
si elle est utilisée à une longuer d'onde inférieure
à une longueur d'onde
nm, devient multimodale
si elle est utilisée à une longuer d'onde inférieure
à une longueur d'onde 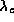 qu'on appelle longueur d'onde de coupure (du deuxième mode). Les
fibre standard des télécommunications ont une longueur d'onde
de coupure
qu'on appelle longueur d'onde de coupure (du deuxième mode). Les
fibre standard des télécommunications ont une longueur d'onde
de coupure 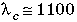 nm.
nm.



