_ _ _ _
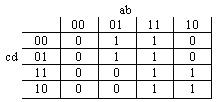
ex: f(a,b,c,d)=abcd + abc + ab + abc
On peut essayer de simplifier son équation à l'aide des
relations de l'algèbre de Boole. Mais on peut aussi représenter
graphiquement cette fonction par son tableau de vérité
:
 |
|
Un tableau de Karnaugh est un tableau de vérité dans lequel les différentes possibilités des entrées sont classées en code GRAY (binaire réfléchi) qui sera détaillé plus loin. Ceci correspond à 0 puis 1 dans le cas d'une variable, 00, 01, 11, 10 pour 2 variables. On peut remarquer qu'en passant d'une case à une case adjacente, une seule variable a changé. Regrouper ces deux cases adjacentes correspond donc à la simplification par cette variable (du fait de l'axiome de complémentation). On simplifie l'équation d'une fonction en faisant des regroupements sous forme d'une, deux ou quatre lignes ou colonnes. Le passage de la dernière ligne à la première est également un cas adjacent (idem pour les colonnes).
En représentant graphiquement une fonction booléenne à n variables, on peut en déterminer une expression simplifiée. Cette simplification est évidente jusqu'à 4 variables, possible avec 5 ou 6 variables (en traitant deux ou quatre tableaux différents supposés superposés). Dans les autres cas, un tableau de Karnaugh permettra toujours de simplifier l'équation, mais jamais au maximum. Par exemple :
_ _ _ _ _ _
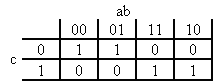
f=a.b.c + a.b.c + a.b.c + b.c + a.c
_ _ _ _ _
donc : f=a.c + a.c + a.b ou f=a.c + a.c + b.c
Remarque : Dans la pratique, si certains cas sont indifférents
(par exemple combinaison de capteurs impossible), on place un X dans le
tableau, que l'on mettra à 0 ou 1 pour simplifier l'expression finale.
On pouvait également regrouper les 0 (s'il y en a moins ou plus groupés) :
_ _ _ _ _ _ _ _ _ f=(a b c)+(a c) d'où f=(a+b+c)(a+c)=ac+ba+bc+a cOn peut également développer la fonction en somme de MINTERMES (forme canonique disjonctive).
- - - - - - -
Dans notre cas : f=a.b.c+a.b.c+a.b.c+a.b.c+a.b.c
Propriétés : Il y a 2n mintermes
d'ordre n (n étant le nombre de variables de la fonction). Deux
mintermes de même ordre ont un produit nul. La somme de tous les
mintermes d'ordre n est 1.L'intérêt de ces décompositions est leur unicité, donc en particulier une programmation facilitée.
exercices : trouver la forme réduite et les formes canoniques des fonctions :
| a) | |
| b) |
question : où cliquer pour la solution ?
___
on notera abc par NAND[a,b,c]
On décompose la fonction sous forme canonique :
(comme vous pouvez le voir, je trouve que j'ai assez travaillé, je garde
mes équations en mode texte bien que ce soit moins beau)
_ _ _ _
f = (abc) + (abc) + (abc)
on peut alors écrire :
_____ _____ _____
_____ _____ _____
_ _ _ _
f = (abc) + (abc) + (abc)
_____________________
_____ _____ _____
_ _ _ _
f = (abc) . (abc) . (abc)
_______ _______ _______
_ _ _ _
f = NAND[ (a,b,c) , (a,b,c) , (a,b,c) ]
_ _ _ _
f = NAND[ NAND(a,b,c) , NAND(a,b,c) , NAND(a,b,c) ]
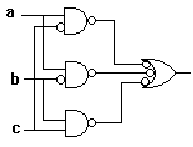
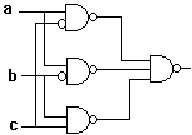
Dans la pratique, les schémas de fonctions définies par ET / OU
se transforment facilement en réseaux composés uniquement de
NAND. Il suffit d'inverser toutes les extrémités des liaisons
internes :
|
|
|