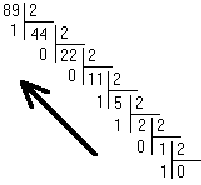
Nous nous limiterons aux applications électroniques (les seules existantes, mis à part l'ordinateur à eau du musée du CNAM).
On peut représenter des nombres par une combinaison de zéros et de uns. Chaque chiffre binaire (BInary digIT) est appelé BIT. 8 bits forment un octet (BYTE). Mais plusieurs codifications sont envisageables. La plus utilisée est le binaire (ou binaire naturel en cas d'ambiguïté).
passage binaire (indice b) -> décimal (indice d) :
1011001b représente :
1x26 +0x25 +1x24 +1x23 +0x22 +0x21 +1x20
=1x64 +0x32 +1x16 +1x8 +0x4 +0x2 +1x1
= 89d
à l'inverse, pour transformer 89d en binaire, on peut utiliser la
méthode des divisions successives
par 2 : on divise successivement par 2 jusqu'à un résultat de 0,
les restes successifs (de bas en haut) forment le nombre binaire.
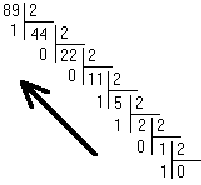
De tête, je ferai : 89 = 1x64 reste 25 donc 0x32, 1x16 reste 9, 1x8 reste 1 donc 0x4, 0x2, 1x1.
On utilise les chiffres 0 à 9 puis les lettres A à F.
3A5h vaut 3x162 + 10x161 + 5x160
=3x256 + 160 + 5 = 933d . On passe de l'hexa au décimal par
divisions successives par 16. Transformer de l'hexadécimal
en binaire est enfantin : il suffit de remplacer chaque chiffre par sa valeur
binaire sur quatre bits : 3A5h = 0011 1010 0101b
(on peut vérifier que ça vaut 933d). En effet,
001110100101b
= 0.211 +0.210 +1.29 +1.28 +1.27 +0.26 +1.25 +0.24 +0.23 +1.22 +0.21 +1.20
= (0.23 +0.22 +1.21
+1.20)28 +(1.23 +0.22
+1.21 +0.20)24 +0.23
+1.22 +0.21 +1.20
=
0011bx28 +1010bx24
+0101bx20
=
3dx162+10dx16+5d
=3A5h
Contrairement à ce que beaucoup de gens croient, aucune machine ne compte en hexadécimal. Elles travaillent toutes en binaire, et ne se servent de l'hexa que pour dialoguer avec nous (nous nous trompons trop souvent dans de longues listes de 0 et 1).
Si vous achetez un voltmètre numérique (69F en supermarché), la valeur mesurée est transmise à l'afficheur en numérique. Mais elle est auparavant transformée en décimal, chaque chiffre décimal est transmis à un afficheur en binaire naturel (sur 4 bits). C'est le BCD : la juxtaposition des valeurs binaires (sur quatre bits) des chiffres décimaux. Donc 583d se notera 0101 1000 0011bcd. Cette codification pose deux problèmes principaux :
On désire qu'en passant d'un nombre à son suivant (+1) ou précédent (-1), on n'aie qu'un seul bit qui change. On désire de plus que les zéro rajoutés à gauche d'un nombre ne soient pas significatifs. Sur deux bits, on utilisera les codes 00, 01, 11 puis 10. Sur 3 bits, on gardera les mêmes premiers codes (précédés d'un zéro). La combinaison suivante débutera donc obligatoirement par 1, donc les deux autres bits ne peuvent pas changer. On continuera à prendre les mêmes codes, en ordre inverse, débutant par 1 : 110, 111, 101 et 100. En passant à 4 bits, on précède ces 8 cas d'un 0, les 8 suivants étant les mêmes, dans l'ordre inverse, précédés d'un 1. Ce codage est utilisé dans les cas où des valeurs ne peuvent varier que par incrémentation ou décrémentation : si l'on voit que plus d'un bit a changé entre deux valeurs, c'est qu'il y a eu un problème (en général le nombre a changé trop vite, le système n'a pas eu le temps de lire toutes les valeurs). Il faut par contre passer en binaire naturel pour tout autre calcul que l'incrémentation.
Un exemple est le capteur de position angulaire (voir transparent T4). Un capteur incrémental comptant des impulsions est utilisé par exemple sur les robots. C'est un disque, entaillé d'encoches régulièrement espacées, passant devant un capteur optique. Certaines impulsions trop rapprochées peuvent être "oubliées" en cas de choc par exemple, et donc occasionner un mauvais réglage. A l'initialisation et en cas de problème, on doit ramener toutes les articulations en position de repos, puis mettre les compteurs à 0, avant de pouvoir utiliser le robot. Un capteur absolu quand à lui donne toujours le position exacte (bien qu'il y ait souvent une démultiplication, le mouvement total fait plus d'un tour mais aucun choc ne fera sauter le capteur d'exactement un tour). On utilise un code binaire réfléchi car un autre codage nécessiterait, pour passer d'une valeur à la suivante, une modification simultanée de plusieurs bits (voir explication sur T4)
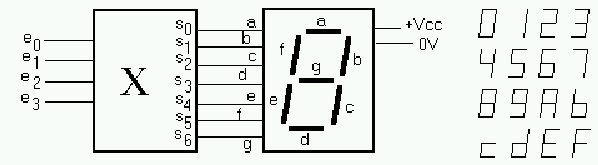
En utilisant plusieurs afficheurs, on affichera un nombre binaire en hexa ou un nombre BCD en décimal, pour des nombres de bits supérieurs à 4
étudier le circuit : (transparent T3)
_ _ _ _
s= r NOR 2 ; 2= a NOR b = a.b ; r= 3 NOR 4 ; 3= b NOR b = b ; 4= a
|
a
|
b
|
r
|
s
|
|
|
0
|
0
|
0
|
0
|
| 0
|
1
|
0
|
1
| |
| 1
|
0
|
0
|
1
| |
| 1
|
1
|
1
|
0
|
_ _ donc r = ba ; s= ba + abc'est donc un additionneur binaire. (s=somme r=retenue, 0+0=0, 1+0=1, 1+1=0 et je retiens 1).
Exercice : faire le même composant uniquement avec des NAND.
A l'aide de ce composant, on peut maintenant faire un additionneur sur plusieurs bits (en général au moins 8, analysons ici uniquement le cas de 3 bits).
a2 a1 a0
|
|
| +
b2 b1 b0
|
-> r0, r1, r2 sont les retenues intermédiaires
|
| r3
s2 s1 s0
|
Trouver le schéma d'un composant admettant en entrée un nombre binaire naturel, donnant en sortie son équivalent en code binaire réfléchi. On se limitera aux nombres de 3 bits. On peut trouver g1 et g0 par tableau de Karnaugh:
---+------+------+ |b2b1b0|g2g1g0| ---+------+------| 0 | 0 0 0| 0 0 0| 1 | 0 0 1| 0 0 1| g2 = b2 2 | 0 1 0| 0 1 1| __ __ 3 | 0 1 1| 0 1 0| g1 = b2.b1 + b2.b1 = b1 XOR b2 4 | 1 0 0| 1 1 0| __ __ 5 | 1 0 1| 1 1 1| g0 = b1 b0 + b0 b1 = b0 XOR b1 6 | 1 1 0| 1 0 1| 7 | 1 1 1| 1 0 0| -----------------+
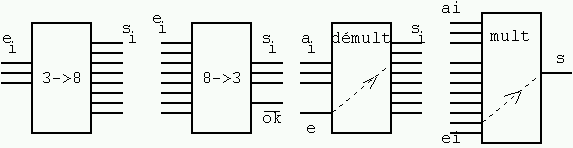
Le décodeur 3 dans 8 comporte 3 entrées e0 à e2, 8 sorties s0 à s7. Il allume une et une seule sortie à la fois, celle correspondant à la valeur binaire donnée en entrée (dons entre 0 et 7, ce qui fait entre 000 et 111 en binaire). A l'inverse, un encodeur 8 dans 3 pose quelques problèmes : quelle sortie donner si plusieurs entrées sont allumées ? On prévoit en général soit une priorité, soit une sortie supplémentaire signalant l'erreur.
Le multiplexeur (voir transparent T6) comporte 2n (ici 8) entrées d'information