COURS SUR LA LOGIQUE
COMBINATOIRE
Systèmes combinatoires
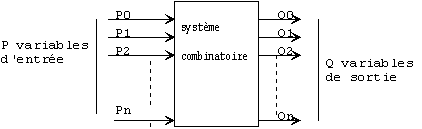
| Un système est dit "combinatoire" lorsque qu'à une combinaison des variables binaires d'entrée correspond une seule combinaison des variables de sorties. |
(note: on parle de systèmes combinatoires par opposition aux systèmes séquentiels ,dans lesquels les variables de sortie dépendent à la fois des variables d'entrée et de l'état antérieur des variables de sortie)

Les systèmes combinatoires interviennent dans la plupart des réalisations électroniques et peuvent être réalisées à partir de nombreuses solutions technologiques.
Le choix de ces solutions dépend essentiellement de la complexité du système à réaliser .
parmi ces solutions , on peut citer :
· les associations diodes-résistances
· les portes logiques
· les circuits logiques combinatoires intégrés (décodeurs , multiplexeurs..)
· les circuits arithmétiques intégrés (additionneurs , multiplicateurs ..)
· les réseaux logiques programmables .
· les mémoires (ROM ,PROM, OU EPROM).
3.2 Conception de systèmes de nature combinatoire
La réalisation d'un système combinatoire nécessite un cahier des charges dont l'énoncé permet ,en détaillant chaque étape du fonctionnement, de dresser un tableau descriptif complet de tous les états binaires .
Ce tableau est appelé "table de vérité" .
De cette table de vérité on peut tirer une expression booléenne qu'il convient de simplifier afin de réduire la complexité de la réalisation.
Il existe plusieurs méthodes d'extraction et de simplification des équations booléennes.
Pour chaque variable de sortie figurant sur la table de vérité, on écrit la "somme" logique des lignes ou la variable de sortie prend la valeur 1.
note: Lorsque les états "1" sont moins nombreux que les états "0", il est avantageux d'écrire le complément de la somme logique des lignes où la variable de sortie prend la valeur 0.
Puis on simplifie l'expression obtenue en utilisant les propriétés de l'algèbre de BOOLE.
Cette méthode peut convenir pour les cas où le nombre de variables d'entrée ne dépasse pas 2 ou 3
exemple de table de vérité de s = f(a,b,c)
| c | b | a | s | |
| 0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 0 0 1 0 1 1 1 |
Extraire l'expression de s ,puis la réduire en utilisant les propriétés de l'algèbre booléenne |
2ème méthode: Utilisation des TABLEAUX DE KARNAUGH
Les tableaux de KARNAUGH sont une représentation particulière de la table de vérité. Les cases représentant l'état des variables d'entrée doivent être adjacentes ( Une seule variable change d'état -> Code Gray).
Les cases vides représentent l'état de la sortie en fonction des variables d'entrée. L'équation de la sortie est une somme de termes, chaque terme étant un regroupement.
Dans un tableau de KARNAUGH, Les regroupements s'effectuent par 2n cases, symétriquement par rapport aux axes de construction du tableau ,les + grands regroupements donnant les équations les + simples .
Représentation des fonctions booléennes par les tableaux de KARNAUGH:
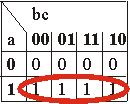
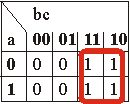
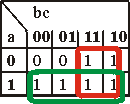
Compléter les tableaux vides
 |
 |
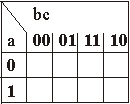 |
| S = a | S = b | S = c |
 |
 |
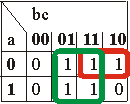 |
| S = a + b | S= a + b.c | S= c + /a.b |