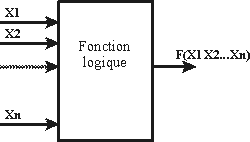
Fonction logique de n variables binaires : groupe de variables reliées par des opérateurs logiques (NON, ET, OU)
Auteurs : Gilles Bouvier et Génaël Valet
L’ensemble des opérations découlant de ces propositions forme une structure mathématique, donc une algèbre , appelée " algèbre de BOOLE " .
Variable logique : grandeur , représentée par un identificateur (lettre ou nom) qui peut prendre les seules valeurs 0 ou 1 .
Algèbre de BOOLE : Ensemble de variables à 2 états ,de valeur ,ou état "1" (vrai) ou 0 (faux) et muni d'un petit nombre d'opérateurs fondamentaux : NON,ET, OU
Fonction logique de n variables binaires : groupe de variables reliées par des opérateurs logiques (NON, ET, OU)

Une table de vérité est un tableau regroupant toutes les combinaisons de valeurs (0 ou 1) que peuvent prendre les variables binaires X1,X2..Xn
Exemple:
| x | y | s |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
1.3 Opérateurs logiques fondamentaux:
Opérateur
"NON"
S est faux si e est vrai
S est vrai si e est faux
| Symbole | Equation booléenne |
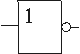 |
table de vérité
| E | S |
| 0
1 |
1
0 |
| A | B | S= A.B |
| 0
0 1 1 |
0
1 0 1 |
0
0 0 1 |
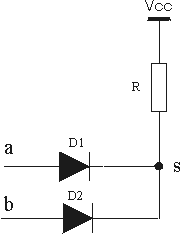
La fonction ET de 2 ou plusieurs variables prend la valeur 1 si toutes les variables sont simultanément à 1
Symbole électrique :
Interprétation électrique :
Il apparaît que la lampe L n’est alimentée que si les interrupteurs a et b sont fermés simultanément
On peut réaliser des fonctions ET à l’aide d’associations diodes-résistances
Opérateur "OU"
| A | B | S= A+B |
| 0
0 1 1 |
0
1 0 1 |
0
1 1 1 |
Interprétation électrique :Symbole électrique :
Exercice : Montrer que la structure ci-dessous constitue un "OU" logique
Il apparaît que la lampe L est alimentée si au moins un des interrupteurs est fermé.
Propriétés
des opérateurs "Et", "Ou"
| propriétés | ET | OU | Applications | |
| COMMUTATIVITE | A.B = B . A | A + B = B + A | Les entrées d’un opérateur logique sont interchangeables | |
| ASSOCIATIVITE | (A.B).C = A.B.C | (A+B)+C = A + C + B | Une fonction ou à 3 entrées peut être réalisée à partir d’opérateurs à 2 entrées. | |
| DISTRIBUTIVITE
OU par rapport au ET ET par rapport au OU |
A
+ (B.C) = (A+B)(A+C)
A.(B+C) = A.B + A.C |
|||
| ELEMENT NEUTRE | A.1 = A | A+0 = A | ||
| table de vérité | symbole | Equation booléenne | |
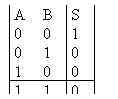
| S est faux si a et b sont vrais | 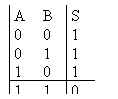 |
| table de vérité | symbole | équation booléenne | |
| S
est faux si a est vrai ou si b est vrai.
S est vrai si a et b sont tous les 2 faux |
 |
Propriétés
des opérateurs "Non et" et "Non ou"
| NON ET | NON OU | Remarques et conclusions pratiques | |
| COMMUTATIVITE | |||
| INVERSIONS | Une fonction NON peut facilement être réalisée à partir d’un opérateur NON ET ou d’un opérateur NON OU , en relianrt une des entrées soit à VCC soit à la masse | ||
| LOIS DE
DE MORGAN |
Ces relations s'avèrent indispensables pour simplifier des équations et les rendre homogènes |
Conclusion
: les opérateur NON ET et NON OU sont universels dans le sens où
leur association permet de réaliser toutes les autres fonctions
booléennes
| table de vérité | symbole | équation booléenne | |
| S est vrai si a est vrai ou b est vrai, mais pas les deux | 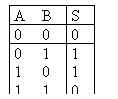 |
Opérateur
"NON OU EXCLUSIF" (XNOR)
| table de vérité | symbole | équation booléenne | ||||||||||||||||
| S est vrai si a et b sont vrais ou si a et b sont faux (quelquefois appelé détecteur d'égalité car s=1 si a=b) |
|
Propriétés:
| XOR | XNOR | |
| COMMUTATIVITE | ||
| ASSOCIATIVITE | Le XNOR n’est pas associatif | |
| PROPRIETES PARTICULIERES |
|
Généralisation:
X1![]() X2
X2 ![]() X3
X3 ![]() ....
.... ![]() Xn = 1si
un nombre impair de variables est à 1
Xn = 1si
un nombre impair de variables est à 1
= 0 si un nombre pair
de variables est à 1