Menu
Général
URL: http://opt-fibres.phys.polymtl.ca/Fibres_html/Fibres.html
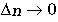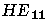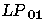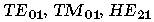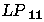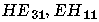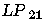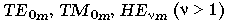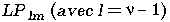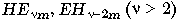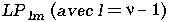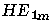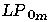| GUIDAGE FORT | GUIDAGE FAIBLE
 |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
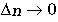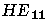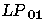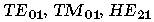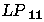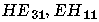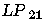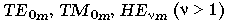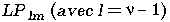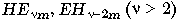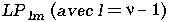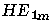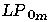Tableau 2.1: Correspondance entre la nomenclature des modes exacts et des modes LP.
Les modes LP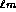
présentent
une dégénérecence d'ordre 2 si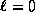 
ainsi que le montre l'exemple de la figure 2.4
dans le cas du mode fondamental LP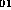
.
Cette dégénerescence est d'orde 4 si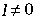
;
la figure 2.5 illustre le cas du mode
antisymétrique LP
.
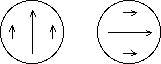
Figure 2.4: Distribution schématique de l'amplitude du
champ électrique du mode LP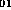
.
Les deux polarisations (le long de x et de y) confèrent
au mode une dégénérescence d'ordre 2.
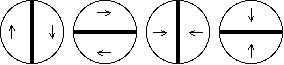
Figure2.5: Distribution schématique de l'amplitude du
champ électrique du mode LP
.
Sa dégénérescence est d'ordre 4.
En guidage faible, les modes LP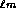
sont des combinaisons de modes exacts (TE, TM et HE) ou (HE et EH); la
figure 2.6 donne schématiquement
un exemple d'une telle combinaison. Il en résulte aussi que les
modes exacts sont en première approximation des combinaisons des
LP
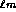polarisés le long
de x ou de y ainsi que le montre la figure 2.7.
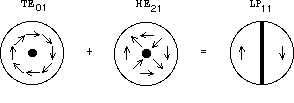
Figure 2.6: Exemple de décomposition d'un mode LP sur la base des modes exacts.
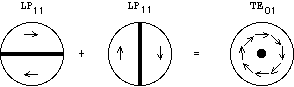
Figure 2.7: Exemple de décomposition d'un mode exact sur
la base des modes LP.