Le but de cette leçon est de montrer quelques principes et problèmes de la conversion analogique / numérique.

Dans cette leçon, on introduit le concept de convertisseur analogique / numérique, une discussion sur la nature des signaux électroniques, ainsi que le théorème d'échantillonnage de Shannon. Ce dernier permet ce cerner une limitation physique à la rapidité d'échantillonnage des signaux analogiques. On passe en revue les principaux types de convertisseurs, en discutant leurs performances. Le chapitre 9 de l'ouvrage "Théorie et traitement de signaux", [3] est consacré à la question de l'échantillonnage de signaux électriques.

1.1. Le convertisseur Analogique/Numérique (CAN)
1.2. Classification morphologique des signaux
1.3.Remarque scientifique: electricité et physique

1.1. Le convertisseur Analogique/Numérique (CAN)
* On dispose d'un signal analogique, dont on voudrait convertir la valeur en un mot numérique, codé en binaire :

* Dans le cas d'un convertisseur dit ratiométrique, le mot binaire en sortie est proportionnel au rapport de la tension d'entrée à une tension de référence :

Si le convertisseur n'est pas spécifié ratiométrique, la tension de référence doit être fixe.

1.2. Classification morphologique des signaux
Nous présentons ici une classification morphologique de signaux, selon qu'ils sont continus ou discrets, dans un temps continu ou discret.

Classification morphologique des signaux :

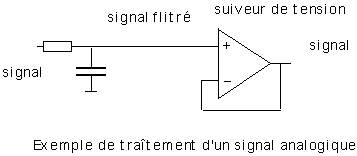
- Le signal analogique peut typiquement sortir d'un amplificateur opérationnel : il évolue dans sa gamme de tension et dans un temps continu.

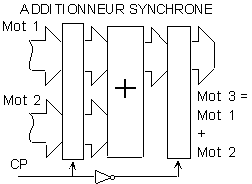
- Le signal numérique est typiquement ce qui se propage dans les systèmes informatiques, où l'information est codée dans un temps discret.

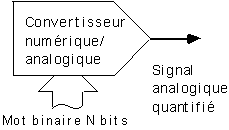
- Un signal quantifié évolue dans un temps continu, mais ne peut prendre que des valeurs de tension quantifiées.

Typiquement, c'est le signal qu'on trouve à la sortie d'un convertisseur numérique / analogique.

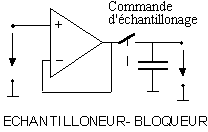
- Un signal échantillonné correspond à la discrétisation du temps appliquée à un signal analogique.

L'échantillonnage d'un signal analogique est souvent une étape de la conversion analogique / numérique.

L'échantillonneur-bloqueur le plus simple est constitué d'un interrupteur de qualité et d'un condensateur se chargeant à la tension voulue.

1.3. Remarque scientifique : électricité et physique

Remarquons que les distinctions présentées précédemment concernant la nature des signaux électroniques sont des outils techniques, permettant d'indiquer où se trouve l'information que l'on véhicule. Du point de vue de la physique classique, tous ces signaux électriques sont analogiques. Mais que sont ces signaux dans les cadres des autres physiques ? Ici, nous nous contenterons d'une remarque générale sous forme d'un micro-panorama pouvant peut-être servir à l'étudiant physicien à situer l'ingénierie électronique

* Nous avons dérivé le modèle de Kirchhoff de l'électromagnétisme. Ce modèle relève donc de la physique classique, cet état de fait s'est illustré avec le bon fonctionnement de l'analogie électromécanique. Le modèle de Kirchhoff se situe donc dans une approche classique objectiviste, c'est à dire observant des faits, sans interaction avec un observateur :

* Or on le sait, en physique dite moderne, l'observateur interfère avec le système observé. Les problèmes de semi-conducteurs et d'optique utilisent généralement la physique quantique. Les relations d'incertitude, la non-commutativité des observables expriment un état de relation entre observateur et observé :

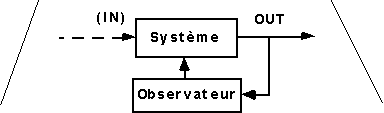
* Dans la nouvelle physique, le paradigme de la thermodynamique est enrichi par l'intégration de la notion d' information :

On voit que, bien qu'amarrée à la physique classique par le modèle de Kirchhoff, l'ingénierie électronique aborde ce qu'il y a de plus récent en physique : la théorie de l'information. Cette information représente ce qu'on obtient d'un système en lui fournissant de l'énergie : de la néguentropie pour l'observateur, de l'entropie pour l'observé. Cette question, de l'ordre du lien entre physique et électricité actuelles est laissée à l'esprit de curiosité et de recherche du lecteur. (Brillouin, Prigogine, ...)

Au chapitre 9 du traité d'électricité Vol 6 : traitement de signal ([12]), il est traité la question de l'échantillonnage de signaux. Du point de vue instrumental, nous devons simplement indiquer ici que :

La cadence d'échantillonnage d'un signal doit être au moins deux fois plus élevée que la plus haute fréquence contenue dans le signal à échantillonner.

Ce résultat est connu sous le nom de théorème de Shannon. Il signifie aussi bien sûr qu'un signal doit voir son spectre limité pour pouvoir être échantillonné : il y a toujours un filtre électronique devant un échantillonneur.

(Cf. Ex. 5.1 : APPLICATION DU Théorème DE SHANNON)

3.1. Convertisseurs à intégration analogique
3.2. Convertisseurs à intégration numérique
3.3. Convertisseurs à approximations successives
3.4. Convertisseurs Flash

3.1. Convertisseurs à intégration analogique
Principe de l'intégrateur à simple rampe :

La tension de référence est intégrée par l'amplificateur opérationnel, puis comparée à la tension à convertir. Le montage logique en aval compte le temps que met la sortie de l'intégrateur à rejoindre la tension d'entrée.

(Cf. Ex. 5.2 : ANALYSE DU CONVERTISSEUR SIMPLE RAMPE)

3.2. Convertisseurs à intégration numérique

Le compteur part de zéro, et compte jusqu'à ce qu'il atteigne une valeur très proche de celle correspondant à la tension d'entrée.

(Cf. Ex. 5.3 : ANALYSE DU CONVERTISSEUR À INTÉGRATION NUMÉRIQUE)

Tracking converter :

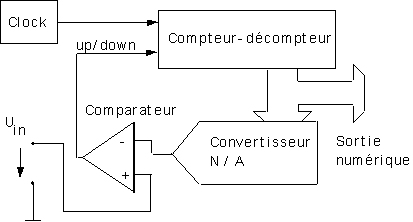
Ici, le compteur ne doit pas compter tout le mot, comme auparavant. Il est capable de compter ou décompter pour atteindre sa valeur.

(Cf. Ex. 5.4 : ANALYSE DU TRACKING CONVERTER)

3.3. Convertisseurs à approximations successives

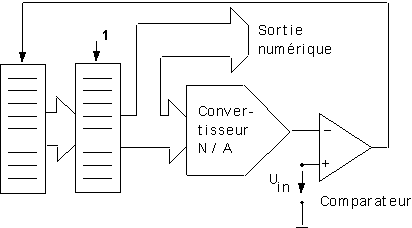
Le registre A est chargé sériellement par un "1", le mot est converti en analogique. Si la valeur numérique est toujours trop petite, il faut placer un "1", sinon il faut placer un "0" dans le registre B. Le contenu du registre B est transféré dans le registre A, puis le cycle recommence.

(Cf. Ex. 5.5 : ANALYSE DU CONVERTISSEUR À APPROXIMATIONS SUCCESSIVES)

Extrait de la fiche technique du DAC 800 :

3.4.Convertisseurs flash
Convertisseur flash à 3 bits :

La tension à convertir est comparée à plusieurs seuils de référence. Le code obtenu est du type :

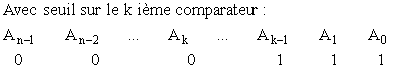
Le décodeur réalise une logique combinatoire pour transformer ce mot en binaire.

(Cf. Ex. 5.6 : ANALYSE DU CONVERTISSEUR FLASH )

4.1. Caractéristiques générales des convertisseurs A/N
4.2. Exemple de convertisseur A/N : le ADC 0800

4.1. Caractéristiques générale des convertisseurs A / N
Les caractéristiques générales des convertisseurs analogique / numérique sont du même type que celles correspondant aux convertisseurs N / A. On peut donc se reporter à la leçon précédente. Nous avons vu néanmoins que le temps de la conversion analogique / numérique peut être plus ou moins important ; c'est donc un élément essentiel dans le choix du convertisseur.

4.2. Exemple de convertisseur A / N : le ADC 0800
Extrait de la fiche technique du convertisseur ADC 0800 de National Semiconductors :

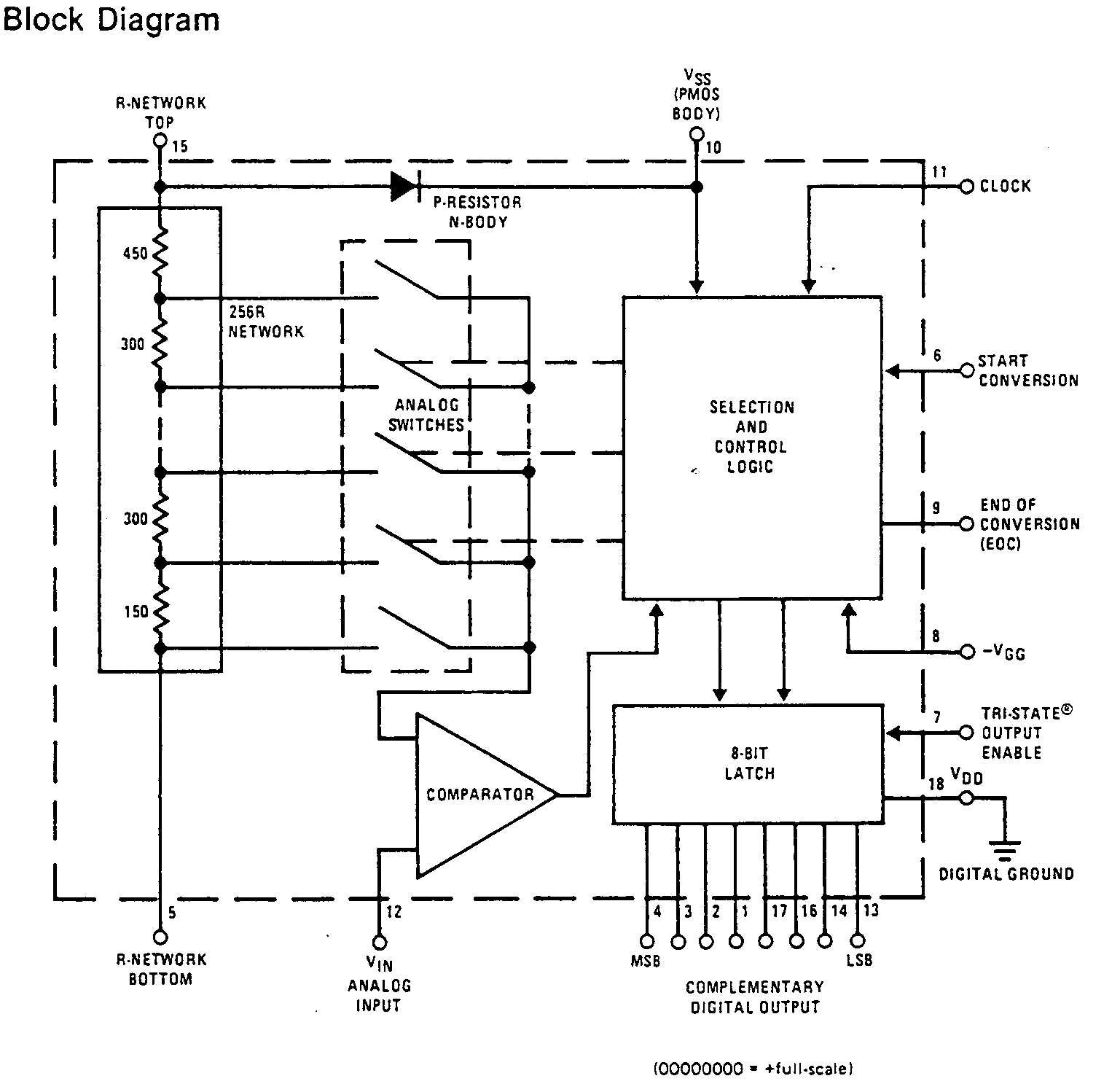
( Cf. Ex. 5.7 FICHE TECHNIQUE DE L'ADC 0800)

Exercice 5.1: Application du théorème de Shannon
Exercice 5.2: Analyse du convertisseur simple rampe
Exercice 5.3: Analyse du convertisseur à intégration numérique
Exercice 5.4: Analyse du tracking converter
Exercice 5.5: Analyse du convertisseur à approximations successives
Exercice 5.6: Analyse du convertisseur flash
Exercice 5.7: Fiche technique de l'ADC 0800

5.1. Exercice: Application du théorème de Shannon

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours
- On veut échantillonner un signal périodique rectangulaire de 100 Hz. A quelle fréquence minimum doit-on échantillonner ce signal, si on veut conserver l'information qu'on trouve dans sa seconde harmonique ? Quel est le problème ?

5.2. Exercice: Analyse du convertisseur simple rampe

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours
Principe de l'intégrateur à simple rampe :

La tension de référence est intégrée par l'amplificateur opérationnel, puis comparée à la tension à convertir. Le montage logique en aval compte le temps que met la sortie de l'intégrateur à rejoindre la tension d'entrée.

- Représentez en fonction du temps les signaux importants (sortie intégrateur, entrée, sortie comparateur, sortie numérique).

- Exprimez mathématiquement la sortie numérique, en fonction des valeurs de composants, de la fréquence et de la référence.

- Quel est le temps requis pour une conversion ?

5.3. Exercice: Analyse du convertisseur à intégration numérique

ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours

Le compteur part de zéro, et compte jusqu'à ce qu'il atteigne une valeur très proche de celle correspondant à la tension d'entrée.

- Représentez en fonction du temps les signaux importants.

- Où intervient la référence ?

- Exprimez mathématiquement la sortie numérique, en fonction de la fréquence et de la référence.

- Quel est le temps requis pour une conversion ?

5.4. Exercice: Analyse du tracking converter

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours
Tracking converter :

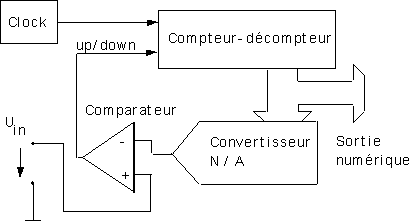
Ici, le compteur ne doit pas compter tout le mot, comme auparavant. Il est capable de compter ou décompter pour atteindre sa valeur.

- Représentez en fonction du temps les signaux importants.

- Où intervient la référence ?

- Exprimez mathématiquement la sortie numérique, en fonction de la fréquence et de la référence.

- Quel est le temps requis pour une conversion ?

- Quel genre de problèmes peut poser ce système asservi ?

- Quelle pente maximum du signal d'entrée peut suivre ce convertisseur ?

5.5. Exercice: Analyse du convertisseur à approximations successives

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours

Le registre A est chargé sériellement par un "1", le mot est converti en analogique. Si la valeur numérique est toujours trop petite, il faut placer un "1", sinon il faut placer un "0" dans le registre B. Le contenu du registre B est transféré dans le registre A, puis le cycle recommence.

- Simulez sur papier les opérations pour un convertisseur 3 bits, avec référence 10 Volts et entrée 5.78 V.

- Exprimez mathématiquement la sortie numérique, en fonction de la référence.

- Quel est le temps requis pour une conversion ?

- Que se passe-t-il si pour cause de bruit, le comparateur fournit une indication erronée au milieu d'une conversion ? Comment minimiser les risques ?

5.6. Exercice: Analyse du convertisseur flash

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours
Convertisseur flash à 3 bits :

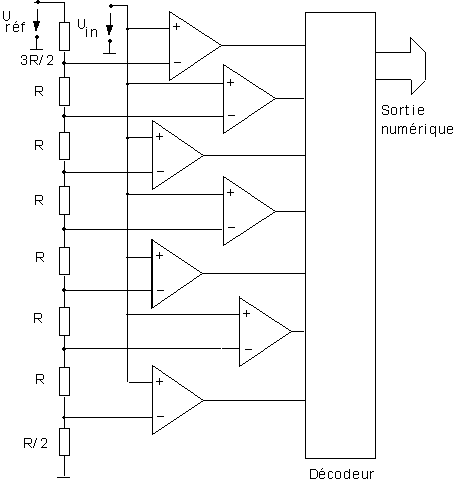
La tension à convertir est comparée à plusieurs seuils de référence. Le code obtenu est du type :

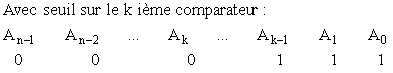
Le décodeur réalise une logique combinatoire, pour transformer ce mot en binaire.

- Réalisez la table de vérité du décodeur à sortie binaire, pour 3 bits.

- Par Karnaugh, trouvez une expression simple de ce décodeur.

- Exprimez mathématiquement la sortie numérique, en fonction de la référence.

- Quel est le temps requis pour une conversion ?

5.7. Exercice: Fiche technique de l'ADC 0800

ÉNONCÉ---Corrigé ---Retour au paragraphe correspondant du cours
- Etudiez la fiche technique de ce convertisseur
- Etudiez les applications typiques présentées dans la notice.

Exercice 5.1: Application du théorème de Shannon
Exercice 5.2: Analyse du convertisseur simple rampe
Exercice 5.3: Analyse du convertisseur à intégration numérique
Exercice 5.4: Analyse du tracking converter
Exercice 5.5: Analyse du convertisseur à approximations successives
Exercice 5.6: Analyse du convertisseur flash
Exercice 5.7: Fiche technique de l'ADC 0800

Exercice 5.1. Application du théorème de Shannon

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours
La fondamentale est à 100 Hz, la première harmonique à 200 Hz et la seconde à 400 Hz. En vertu du théorème de Shannon, on pourrait échantillonner à 1 KHz par exemple. Mais pour cela, il faudrait pouvoir éliminer les harmoniques d'ordre supérieur, ce qui n'est pas forcemment réalisable. En placant un filtre en amont du convertisseur, on peut améliorer la situation, mais en général, c'est un problème de traitement de signal.

Exercice 5.2. Analyse du convertisseur simple rampe

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Indication:

Pour chaque mesure, il faut un temps dépendant de la constante d'intégration ainsi que de la valeur même à convertir:

Exercice 5.3. Analyse du convertisseur à intégration numérique

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Indication:

De même, avec une horloge de fréquence f, le temps d'intégration dépend du mot converti:

Exercice 5.4. Analyse du tracking converter

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Indication:

Le convertisseur n'intègre pas à chaque mesure, mais suit la sortie. Si les problèmes de stabilité de ce système asservi sont maîtrisés, on peut toujours lire sa sortie à une précision qui dépend de la qualité du réglage ainsi que de la rapidité de variation de l'entrée. La pente maximale du mot en sortie dépend de la fréquence d'horloge.

Exercice 5.5. Analyse du convertisseur à approximations successives

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Indication:

Ce convertisseur présente l'avantage d'un faible et fixe temps de conversion : pour 8 bits, 8 fois la période d'horloge. Le problème est la sensibilité au bruit: une erreur détruit le résultat, ce qui n'est pas le cas avec les convertisseurs à intégration qui présentent une immunité au bruit importante. Chaque application doit résoudre ses problèmes: si les erreurs sont intolérables et que ce système en génére trop, on doit changer de type de conversion. Si ce convertisseur est inséré dans un système peu sensible aux erreurs (système asservi par exemple), il présente l'avantage de la rapidité.

Exercice 5.6. Analyse du convertisseur flash

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Indication:

Le convertisseur "flash" est un système combinatoire, donc fonctionnant à la vitesse des composants eux-même. L'inconvénient est le grand nombre de composants.

Exercice 5.7. Fiche technique de l'ADC 0800

CORRIGÉ---Énoncé ---Retour au paragraphe correspondant du cours

Voir la fiche technique de l'ADC0800