RAYONNEMENT DE FRAUNHOFER D’UNE BOUCLE CIRCULAIRE DE COURANT DE DIAMETRE PETIT PAR RAPPORT A LA LONGUEUR D’ONDE . RESISTANCE DE RAYONNEMENT.

PROBLEME

Soit une boucle circulaire (c) rayonnante de diamètre 2a, de centre 0 disposée dans le plan xoy.

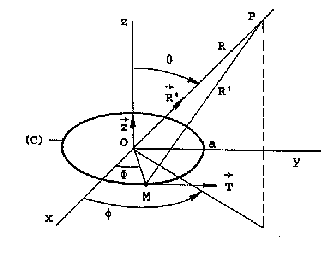
Elle est parcourue par un courant instantané I constant le long de la boucle et variable sinusoïdalement en fonction du temps, de pulsation .

Le milieu dans lequel elle est plongée est de l’air de constantes et .

Les charges statiques étant nulles en tout point de l’espace, le potentiel scalaire est nul.

1. A l’aide du potentiel vecteur retardé au point P supposé à très grande distance (de coordonnées polaires ),déterminer les composantes et du champ rayonné..
2. Montrer qu’à grande distance, la composante est nulle, et que la composante peut s’écrire :

:

On donne les expressions suivantes.

et 

3.Déduire les composantes et du champ magnétique toujours au point P situé à très grande distance.

4.Donner les expressions du champ électromagnétique lorsque le diamètre 2a est faible devant la longueur d’onde. Pour cela, on prendra le développement limité :[sachant par exemple que l’erreur commise est inférieure à 12 % lorsque ].

5.Que peut-on dire alors sur le rayonnement comparé à celui d’un doublet disposé en 0 le long de Oz ?

6.En calculant le flux du vecteur de Poynting à travers une sphère de centre 0 et de grand rayon, montrer que la résistance de rayonnement rapportée au courant I dans la boucle peut s’écrire :

en ohms.

Dans l’approximation de la question n°4 (voir aussi [5]&1.5).

1. Que deviennent les amplitudes des champs E et H et la résistance de rayonnement lorsque l’antenne « boucle » est constituée par N spires circulaires concentriques de diamètre sensiblement égal à 2a, localisées dans le plan xoy , et toutes parcourues par le même courant I. ?
2. .-APPLICATION NUMERIQUE