RAYONNEMENT DE FRAUNHOFER D’UNE BOUCLE CIRCULAIRE DE COURANT DE DIAMETRE PETIT PAR RAPPORT A LA LONGUEUR D’ONDE . RESISTANCE DE RAYONNEMENT.
Retour à l'énoncé

SOLUTION

1.- Soit M le point courant de la boucle défini par ses coordonnées polaires (a,)et le vecteur unitaire de la tangente en M à ( C). Soit R’ la distance de M à P et k le nombre d’onde . Le potentiel vecteur retardé au point situé à grande distance R>>a est donné par l’expression:

(1)

ds est l’élément différentiel curviligne le long de (c ) .Les composantes de sont: 

Par définition on a: et (2)

et sont des vecteurs unitaires dont les composantes sont:

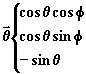
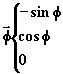
On déduit donc: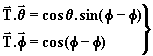(3)

Compte tenu du fait que les charges statiques sont nulles, le champ électromagnétique au point P s’exprime comme suit:(4)

On déduit avec (1),(2) , (3), et (4):

(5)

(6)

A grande distance, on peut écrire:

Les expressions (5) et (6) prennent la forme:

(7)

(8)

2.- Montrons d’abord que est nulle. En effet posons dans l’intégrale (7). Il vient pour cette intégrale: comme varie de 2 le long de ©, l’intégrale est nulle. Donc Calculons l’expression (8). Posons L’intégrale de l’expression (8) devient:

compte tenu des deux expressions données dans l’énoncé. Dès lors, l’expression (8) s’écrit finalement:

(9)

Dans le système MKSA:. On aura donc pour le module de exprimé en volt/mètre:

(10)

Les longueurs étant exprimées en mètres et l’intensité I en ampères.

1. A partir de l’expression(9), on déduit pour le champ magnétique: et 

(11)

Le signe moins provient du fait que le trièdre est direct.

Les expressions (9) et (11) s’écrivent dans le système MKSA:

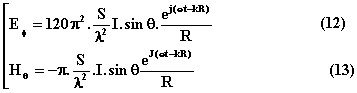
avec aire de la boucle circulaire.

5.Les expressions (12) et (13) sont identiques à celles qui expriment le champ rayonné à grande distance par une boucle de courant de forme quelconque non obligatoirement plane, dont les dimensions sont faibles par rapport à la longueur d’onde, équivalente à un court doublet magnétique dont le moment est porté par Oz,

avec et 

S étant une surface quelconque qui s’appuie sur la boucle.

6. Calculons le flux F du vecteur de Poynting à travers une sphère de grand rayon R centré en O. Comme et sont orthogonaux dans l’espace et perpendiculaires à , on obtient pour F :

En tenant compte des expressions (12) et (13), on obtient dans le système MKSA.:

Comme on déduit finalement en rappelant que:

7.- Les amplitudes des champs sont multipliées par N et la résistance par .

Soit:(15)

On trouve (12),(15):
Retour à l'énoncé