CHAMP ELECTROMAGNETIQUE RAYONNE PAR UN DOUBLET ET RESISTANCE DE RAYONNEMENT. APPLICATION AU DOUBLET DEMI ONDE.

PROBLEME

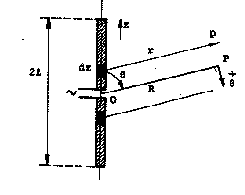
On considère un doublet symétrique mince de longueur 2, isolé dans l’espace vide, parcouru par un courant instantané de la forme avec

et ( : longueur d’onde).

Ce courant est variable sinusoïdalement en fonction du temps.

1.- Calculer le module du champ électrique rayonné à grande distance au point P en fonction de l’angle à l’aide de l’expression du champ rayonné à grande distance par le doublet de Hertz.

2. Que devient l’expression du champ électrique lorsque  ? (où n est un entier positif ou nul).

(doublet à la résonance avec un maxima de courant au point d’alimentation).

3. Tracer avec précision le diagramme de rayonnement pour n=1.

4.- Calculer la puissance dissipée sous forme de rayonnement en intégrant sur la surface d’une sphère de très grand rayon et de centre 0 le vecteur de poynting complexe toujours dans le cas où 

La résolution de l’intégrale s’effectue ra en faisant par successivement les changements variables : et 

Et sachant que :où est la constante d’Euler, et le cosinus intégral de t.

5.-. Déduire de la puissance rayonnée la résistance de rayonnement rapportée au courant maxima I_0.

APPLICATION NUMERIQUE : retrouver la résistance de rayonnement d’un doublet demi – onde (cas n=0)qui est égale à =73,12ohms.

On donne :

6.- Quelle est la relation qui lie la résistance de rayonnement à la directivité maximale ? Retrouver celle du doublet demi mi onde.(n=0).

7 – Donner l’expression de la surface maxima d’absorption du doublet symétrique à la résonance en fonction de sa résistance de rayonnement.
Solution