ADMITTANCE D’ENTREE D’UN DOUBLET PLAQUE A SYMETRIE AXIALE.

PROBLEME

Considérons une antenne plate, symétrique, de forme quelconque dont la hauteur H par rapport au plan réflecteur métallique yoz est très petite par rapport à la longueur d’espace libre. Elle admet le plan xoz comme plan de symétrie (fig.1)

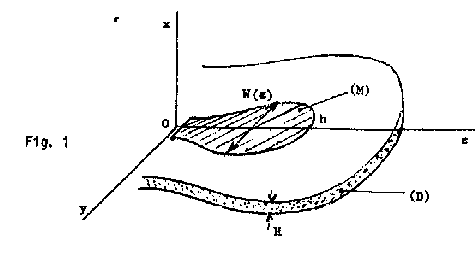
Une couche de diélectrique (D), d’épaisseur constante H et de permittivité relative sépare la plaque métallique rayonnante (M) du plan réflecteur. La largeur de la plaque est une fonction de z, soit (W(z). Une différence de potentiel alternative de pulsation est appliquée entre le bord de l’antenne W(0) et le plan réflecteur . Nous supposons un mode TM relativement à l’axe ox, donc correspondant à , et un champ électrique parallèle à l’axe ox.

1.- Montrer en l’absence de rayonnement, c’est – à- dire dans l’hypothèse d’un champ électromagnétique strictement confiné entre (M) et yoz que l’unique composante du champ électrique vérifie l’équation suivante:

(1)

désigne le Laplacien Transversal relativement à l’axe ox..

et k₀ est le nombre d’onde d’espace libre:.

2.- Pour tenir compte du rayonnement et éventuellement des pertes métalliques et diélectriques dans l’antenne. On désigne la permittivité relative effective .

Montrer, lorsque , condition impliquant que les uniques composantes E_x et du champ électromagnétique sont indépendantes de la variable y, les relations suivantes:

(3) (4)

est l’admittance du milieu vide: et est la conductance caractéristique de l’antenne.

.3.- Selon les hypothèses de la question n° 2 et à l’aide de (3) et (4) démontrer que l’admittance:

est une solution de l’équation générale de riccati suivante et rappelée en III.G. (77):

(5)

4- Que devient l’équation (5) dans le cas d’une antenne plaque rectangulaire sachant que ne dépend plus de z?

Peut-on la résoudre pour aboutir à une forme analytique?

En déduire l’admittance d’entrée (z=0).
Solution