ADMITTANCE D’ENTREE D’UN DOUBLET PLAQUE A SYMETRIE AXIALE.
Retour à l'énoncé

SOLUTION

1.- Comme le champ électrique est parallèle à l’axe Ox, nous avons :. L’onde est TM relativement à Ox. Nous déduisons : et . Les équations de Maxwell s’écrivent :

entraînant 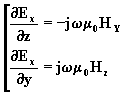(6)

entraînant (7)

En combinant (6) et (7), il vient :

1. – Nous avons :avec 

entraînant Hz=0.

Le courant axial I(z) et la tension V(z) sont donnés par les expressions :

et 

On déduit de la théorie des lignes de transmission [(75) et (76) de III.G] :

d’où l’on déduit aisément les relations (3) et (4) à savoir :

, 

3.- Soit l’admittance : 

En dérivant on écrit successivement :

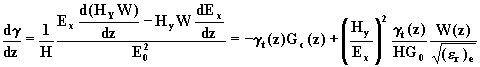
On obtient finalement l’équation (5) :

4. – Dans le cas d’une plaque rectangulaire , on a : et 

L’équation (5) devient : dont la solution générale, compte tenu de la condition aux limites : est la suivante : 

On rappelle que la constante linéique qui tient compte des pertes par le rayonnement et des pertes métalliques et diélectriques est donnée par l’expression (73) du paragraphe III.G.
Retour à l'énoncé