ADMITTANCE DE RAYONNEMENT ET BANDE PASSANTE D4UN DOUBLET PLAQUE RECTANGULAIRE.

PROBLEME

Soit un doublet plat rectangulaire (figure 10 du rapport théorique III H). Sa largeur est W, sa longueur h, la permittivité relative du substrat est , et la résistance caractéristique de la ligne de transmission équivalente.

2.- Dans l’hypothèse du fonctionnement en mode quasi TEM l’impédance de rayonnement du doublet, supposé d’abord sans pertes ohmiques ( =0 et =0). Et rapportée à l’entrée z=0 est égale à :

(1)

a coefficient réel qui tient compte du rayonnement et nombre d’onde. En développant l’expression (1), on trouve :(2)

(3)

Sachant que la résistance de rayonnement d’un doublet isolé, dans le milieu air (King [8]) est égal à :

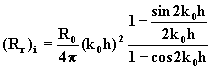(4)

et qu’en présence d’un plan réflecteur , de dimensions infinies, et correspondant au milieu air (), cette résistance de rayonnement devient égale à [9]. :

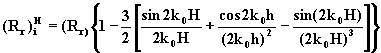(5)

montrer en identifiant (2) avec (5) dans l’hypothèse , et dans le milieu air, que la constante linéique d’atténuation a due au rayonnement est donnée par l’expression suivante :

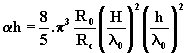(6)

2.- Toujours dans l’hypothèse des pertes ohmiques nulles, montrer à l’aide de (6) supposé valable dans un milieu , que la conductance de rayonnement à la résonance demi – onde () est égale à l’expression (7) :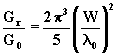(7), la résistance caractéristique R_c étant donnée par l’expression (7 8) du paragraphe III H, soit : dans l’hypothèse où W/H>>1 et .

3.En tenant compte des pertes dans le diélectrique et dans le métal ramenant à l’entrée du doublet plat les conductances de pertes suivantes :(8) (9)

retrouver les résultats donnés dans le rappel théorique III.G formules (8.2) et (83). est l’angle de pertes du diélectrique.

4.- Déduire que l’efficacité de rayonnement du doublet plaque est donnée par l’expression :

Solution