INTERFERENCES DE N SOURCES COHERENTES EQUIPHASES D’AMPLITUDES DIFFERENTES
Retour à l'énoncé

SOLUTION

1. L’amplitude réelle des champs dont les courants des sources correspondantes en nombre n pair sont :

avec et longueur d’onde .

Introduisons les polynômes de Tchebyscheff 

En posant : 

L’amplitude du champ total s’écrit donc :

La méthode de recherche d’une distribution optimum de Dolph Tchebyscheff consiste à identifier R(x) à un polynôme , avec et où est donné par .

Avec 

(Les lobes secondaires étant alors tous égaux).étant >1, 

On déduit :

L’identification de R et conduit nécessairement à l’expression de en fonction des polynômes de Tchebyscheff et de Z₀..

2.- Cas particulier :n=12, 

D’après ce qui précède, on aura à identifier en x l’expression :

On a donc :

.

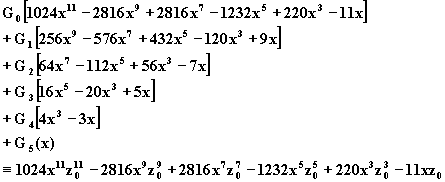
En identifiant, on obtient les 6 équations :

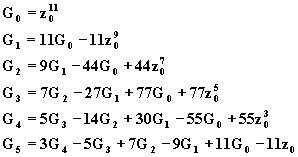
3.n=12, on obtient à partir de la valeur :

D’où : 

On tire donc des équations précédentes :

=3,41 =7,6 =13,9 =21,4 =28,5 =32,8

On trouve en normalisant les courants des sources :

=0,105 =0,232 =0,424 =0,653 =0,87 =1

1. Le demi angle entre directions à ½ puissance est donnée par :

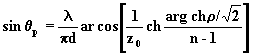avec z₁=1,118, =100, n=12, , on obtient :

soit 

Les directions de rayonnement nul sont données par :

Or ceci est nul pour :

ou

soit 

et 

Mais

D’où l’on obtient :

On obtient les angles correspondant à un champ nul :pour k=0=11°,1

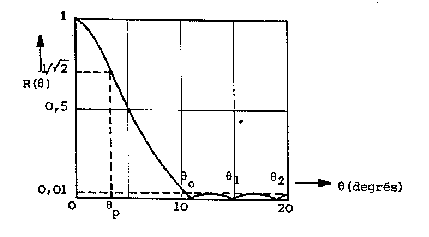
5.Il n’y a qu’un lobe principal pour variant de 0 à si :

soit si 

C’est à dire 
Retour à l'énoncé