INFLUENCE DE L’EPAISSEUR D’UN DOUBLET SUR SA FREQUENCE DE RESONANCE. APPLICATION A LA FENTE RAYONNANTE COMPLEMENTAIRE.
Retour à l'énoncé

SOLUTION

1. La réactance d’entrée de la ligne équivalente au demi doublet est telle que:




A la résonance pour laquelle , on a:



soit 

Comme ,

On déduit: (6)

Par définition nous avons ([5] chapitre 3, paragraphe3.1):



Compte tenu de l’expression (6), on trouve le facteur de raccourcissement K demi doublet à la résonance, soit:(7)

2. En explicitant le paramètre d’expansion de Hallên, soit , on trouve à partir de (7) l’équation transcendante suivante

(8)

On peut réduire cette équation par approximations successives à partir d’une valeur approchée obtenue en effectuant un développement limité (faible ). On trouve les résultats présentés dans le tableau ci dessous:


2. Pour , on trouve pour la résistance de rayonnement du demi doublet à la résonance la valeur suivante:

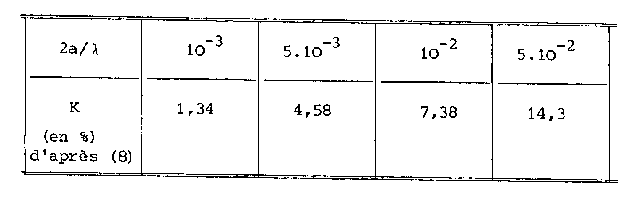
Cette valeur est très proche de celle obtenue par la méthode de résolution de l’équation intégrale de Hallên.

La formule (5) exprimée en ohms s’écrit:

Avec à la première résonance, on obtient finalement:

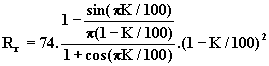(9)

Pour les valeurs précédents de , on obtient le résultat suivant:

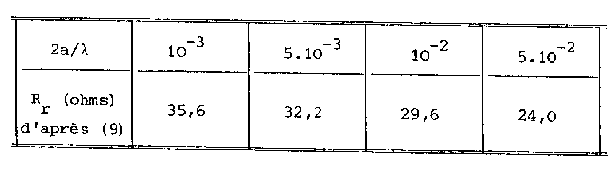
CONCLUSION: A la fréquence de première résonance, plus le demi doublet a un diamètre grand par rapport à la longueur d’onde plus la résistance de rayonnement est faible.

3. Le principe de Babinet nous permet d’écrire:

:est l’impédance de rayonnement du doublet symétrique.

A la résonance on aura:

Comme il s’agit d’un doublet symétrique, on a:et l’expression générale de est la suivante: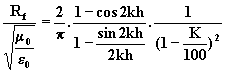(10)

AN.: Calculer les dimensions de la fente et la résistance de rayonnement pour f=10GHz, ,

On trouve facilement:K=4,58

Soit 
Retour à l'énoncé