Menu Général                                     URL: http://antares.rio.net/cameroun/EAO/exca1.htm

RAYONNEMENT DU DOUBLET CYLINDRIQUE ISOLE DANS L’APPROXIMATION SINUSOIDALE.

SOLUTION
Retour à l'énoncé

  1. Cette résistance 
est donnée par l’expression: (1) C’est la résistance d’entrée d’une ligne ouverte de longueur et d’impédance caractéristique exprimée en ohms égale à , où est l’impédance d’onde du milieu ; est le paramètre d’expansion de Hallen:

, k est le nombre d’onde:.

2.- La loi de distribution de courant du type sinusoïdale est de la forme:

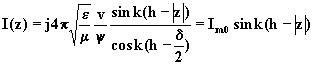(2)

Le courant est nul aux extrémités du double

3.- A grande distance le champ électrique est purement transversal et porté par l’axe dont le vecteur unitaire est .

(3)

avec 

est le vecteur unitaire de la direction OP

est le vecteur unitaire de l’axe OZ.

On a: 

L’expression (3) s’écrit donc:

soit compte tenu de (2);

expression que l’on peut encore écrire:

Comme , on peut étendre la borne inférieure de l’intégrale à 0.

D’autre part , on a:

d’où (4)

ou encore compte tenu de la valeur de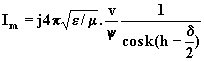 

4.- La résistance de rayonnement Rr rapportée au courant à l’entrée soit sensiblement

, s’écrit:

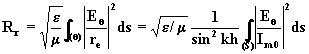
où S est la sphère de rayon grand par rapport à la longueur d’onde centrée au point 0 (théorème de Poynting).

On peut encore écrire:

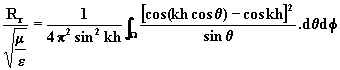
variant de 0 à et de 0 à 2. Compte tenu de la symétrie de révolution, on peut écrire finalement:

(5)

5.-Si , on peut faire un développement limité et écrire en se limitant au premier terme:

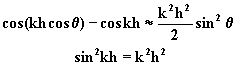
L’expression (5) s’écrire alors:

Soit encore:

Et en calculant l’intégrale:(6)

Dans le vide ou l’air:

On peut calculer le coefficient de surtension:

Avec Rr donné par (6) et Xr par (1)

Un calcul simple conduit à l’expression: (7)

6.-. Pour , et l’expression (5) devient:

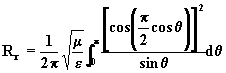
soit 

A.N.:

Milieu vide ou air:et =73,14 ohms.
Retour à l'énoncé