RAYONNEMENT DU A UNE CHARGE ELECTRIQUE PONCTUELLE ACCELEREE

SOLUTION
Retour à l'énoncé

1. Comme la trajectoire ( c) est à grande distance de o, on peut supposer que OP et 

1-A) Par définition, on a pour la composante radiale de la vitesse :

avec (1)

On déduit :(2)

1-B) Par définition, on a :

et en tenant compte de (1), on peut écrire ,

(3)

1.- c) En projetant la relation vectorielle (3) sur OP ou sur , on a :

(4)

2.- L’onde arrivant à l’instant t au point 0 est issue du point 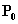. On a donc :

ou encore avec (2) :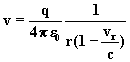

et comme , on peut encore écrire :

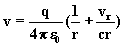(5)

De même, le potentiel vecteur au point 0 et à l’instant t, est tel que :

Avec (2) et l’approximation déjà faite 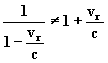, on déduit :

(6)

3. Par définition, on a pour le champ électrique au point 0 :

(7)

et v étant les potentiels vecteur et scalaire définis par (6) et (5).

On obtient :

Or

ou bien, compte tenu des relations données dans l’énoncé :

En utilisant la relation (4) sous la forme : on peut écrire finalement en négligeant devant 1 :

Avec 

Puisque , on déduit : 

D’où finalement l’expression du champ électrique donnée par (7) :

L’un des termes est du type coulombien dirigé suivant , soit :

dont l’amplitude varie en .

Les deux autres termes peuvent s’écrire :

(8)

puisque 

C’est le champ électrique rayonné et dû à l’accélération de la charge.

Or . étant l’accélération tangentielle.

L’expression (8) s’écrit encore :

(9)

4. Le champ magnétique est tel que :

soit d’après (6) : 

soit 

Or on peut décomposer :

D’où :.

Le terme est celui de la magnétostatique, et

En utilisant l’expression (3), on a :

puisque car vitesse à l’origine est constante.

Or 

On suppose :

D’où finalement :,

C’est – à – dire :

Or 

Donc :(10)

C’est le champ magnétique rayonné dû à l’accélération de la charge.

5.- Les expressions (9) et (10) montrent immédiatement que le trièdre est direct (voir fig.1). Le rapport des amplitudes des champs électrique et magnétique dûs à l’accélération de la charge est le suivant :

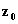étant l’impédance du vide égale dans le système SI à 120 soit 377 ohms.
Retour à l'énoncé