1 Rappels d'électronique numérique
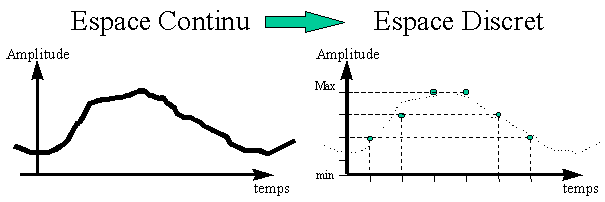
La numérisation d'un signal analogique se traduit par un changement de représentation de ce signal depuis un espace à N dimensions continument variable selon ses axes vers un espace de même dimension qui n'est continu selon aucun de ses axes.
En théorie, le signal, d'origine physique, est assimilable à une suite infiniment grande de points pouvant prendre une infinité de valeurs ; en réalité, la notion d'infini peut être ramenée à des notions plus perceptibles telles que la résolution ; elle correspond à la plus petite variation du signal selon chacune des N dimensions de son espace d'origine perçue par le destinataire de l'information.
Fig. 1.1 : Numérisation d'un signal
On peut alors considérer différemment les opérations de numérisation suivant les caractéristiques des axes traités :
1 Le signal occupe, suivant l'axe, un espace borné : Quantification
Ce changement d'espace, rencontré dans la quantification d'un signal (axe des amplitudes), est analogue à une modulation, il donne certaines propriétés au nouveau signal dont la plus connue est la représentation par une suite numérique interprétable par un calculateur. La plus petite variation perçue déterminera le quantum de représentation de l'information ; ce quantum peut être interprêté comme la limite en dessous de laquelle toute information supplémentaire n'est pas perceptible, et est donc inutile.
2 Le signal occupe, suivant l'axe, un espace infini : Échantillonnage
Ce changement d'espace n'est rencontré que suivant l'axe temporel, seul axe physique à ne pas être borné, on réalise donc un échantillonnage (ou une discrétisation) correspondant à l'analyse du signal à certains instants ; on considère alors le plus petit intervalle de temps tel qu'une variation maximale du signal soit correctement représentée dans l'espace de destination. Cette quantité correspond en fait à la bande passante du signal à numériser et est régie par le théorème de Shannon, également connu comme le théorème de l'échantillonnage sur lequel nous reviendrons dans le courant de ce chapitre.
Afin de bien appréhender les 2 opérations élémentaires de la numérisation du signal analogique que sont l'échantillonnage et la quantification, nous les étudierons séparément pour bien mettre en évidence l'incidence de leur utilisation sur le signal.
La définition de tout traitement effectué sur un signal doit passer par la prise en compte des caractéristiques et des performances de l'organe de destination ; on peut illustrer cela par 2 exemples touchant à l'image :
Traitement d'images (reconnaissance de formes, segmentation) :
La numérisation du signal doit permettre à un calculateur d'extraire les informations suffisantes pour appliquer correctement l'algorithme considéré ; le premier traitement à effectuer consiste alors à éliminer les artefacts générés par la numérisation par filtre numérique (passe-bas) ; dans ce cas, on pourra évaluer concrètement les distorsions et bruits apportés la numérisation.
Télévision (et autres systèmes audiovisuels)
L'influence de la numérisation sur le signal est alors jugée par un observateur, lequel possède des caractéristiques de perception subjectives ; dans ce cas, la numérisation ne doit pas générer, dans la mesure du possible, de défaut perceptible par l'observateur. Il faut garder à l'esprit que la perception humaine des phénomènes physiques reste analogique et donc que le résultat de tous les traitements appliqués au signal n'ont de sens que si l'on sait revenir dans l'espace d'origine, celui qui nous est perceptible.
La technique de l'échantillonnage consiste à prélever pendant un temps très court la portion correspondante du signal à numériser ; l'opération est réalisée, généralement suivant une échelle régulière suivant l'axe de temps, avec une période de répétition de Te. Soit les notations suivantes :
s(t) : signal analogique
s*(t) : signal échantillonné
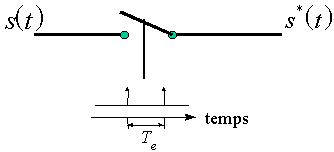
Fig. 1.2 : Échantillonnage d'un signal
L'opération d'échantillonnage ainsi réalisée correspond à la convolution de s(t) avec e(t) (fonction d'échantillonnage), ce qui est exprimé par la formule suivante :
avec 
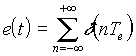: fonction d'échantillonnage (distribution de dirac)
Il en découle la relation suivante entre les transformées de Fourier de chacun des signaux élémentaires, donnant le spectre du signal échantillonné :
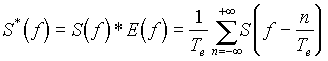
L'allure du spectre est donnée par la figure 1.3, cela correspond à la duplication du spectre du signal d'origine sur tous les harmoniques de la fréquence d'échantillonnage ; on retrouve donc le spectre dit de base (celui du signal d'origine) entouré de spectres "images" que l'on appellera "spectres parasites" pour éviter toute confusion avec l'image (celle que l'on observe sur un écran !).
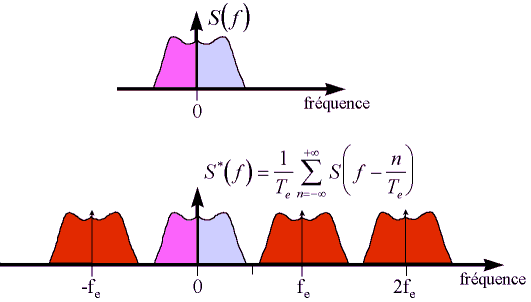
Fig. 1.3 : Spectres des signaux analogique (S(f)) et échantillonné (S*(f))
L'analyse de l'échantillonnage qui vient d'être faite est purement théorique car il n'est pas physiquement possible de réaliser la fonction dirac. Le propos de ce document n'est pas d'analyser l'échantillonnage sous toutes ses formes, aussi nous nous contenterons seulement d'analyser un cas extrême. Supposons que la fonction d'échantillonnage soit un échelon (à la place d'un dirac, cela veut dire que, pendant toute la période d'échantillonnage, on maintient (bloque) le signal de sortie ; le spectre du signal bloqué est alors illustré par la figure 1.4 ; il ressort que les raies parasites sont atténuées par la fonction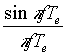 
, ce qui est plutôt intéressant mais il s'avère que le spectre de base subit également une légère atténuation par la même fonction, ce qui peut être gênant.
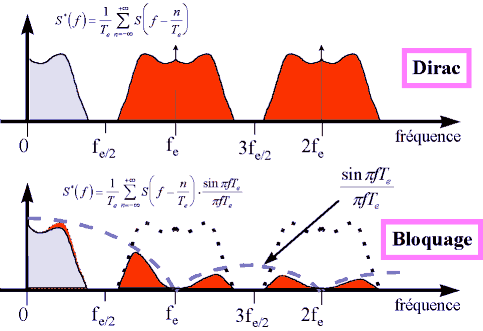
Fig. 1.4 : Spectres issus de l'échantillonnage (dirac) et du blocage
Une des spécifications de l'échantillonnage est de permettre, après traitement, de restituer le signal d'origine sans altérations ; le blocage induit un phénomène de filtrage passe-bas mais n'apporte pas de distorsions. Par contre, si le spectre de base du signal d'origine présente des composantes spectrales au-delà de fe/2, l'échantillonnage, par le jeu des spectres parasites, va les ramener vers les basses fréquences symétriquement à fe/2 ; on aura alors distorsion par repliement de spectre, altération impossible à corriger par traitement ; dans ce cas, le théorème d'échantillonnage (ou théorème de Shannon) n'est pas respecté.
Supposons le signal correctement échantillonné. Pour le restituer, il faut éliminer, par filtrage passe-bas, les spectres parasites ; le filtre idéal est celui dont la réponse spectrale vaut 1 de -fe/2 à + fe/2, ce qui correspond à la transmittance :
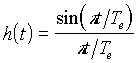
La reconstruction du signal peut alors s'écrire :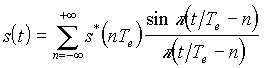 
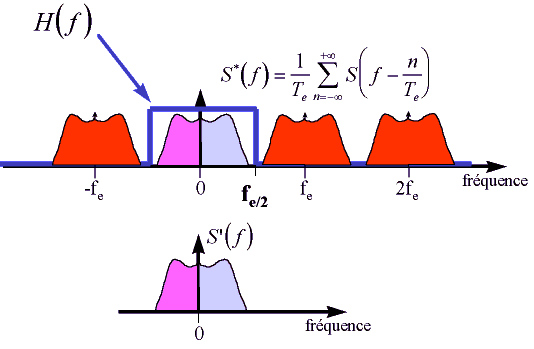
Fig. 1.5 : Reconstruction d'un signal échantillonné
La quantification consiste à représenter la valeur instantanée d'un signal par un nombre sur une échelle possédant un nombre fini de valeurs ; le signal peut être continument variable (signal échantillonné, par exemple) ou un signal discret (déjà quantifié).
Cette opération consiste donc une approximation d'une valeur (ou d'un nombre) appartenant à un ensemble continu (ou non) borné, c'est à dire pouvant prendre une infinité (ou un grand nombre) de valeurs comprises entre un minimum et un maximum, par un nombre appartenant à un ensemble discret borné ne pouvant prendre qu'un nombre fini de valeurs.
La quantification d'un signal consiste à appliquer aux échantillons de s(t) un traitement non-linéaire qui leur fait correspondre une valeur discrète sq(t) ; le signal quantifié sq(t) représente alors le signal s(t) à l'erreur de quantification e(t) près : 
; le signal e(t) est assimilable à du bruit rajouté au signal par l'opération de quantification, on parlera alors de bruit de quantification.
Le quantum entre 2 valeurs discrètes est appelé échelon de quantification (noté q), si celui-ci est constant (c'est très souvent le cas sauf en audio), le quantificateur est dit uniforme. Dans le cas d'une quantification uniforme binaire sur N bits d'un signal évoluant dans la plage 
, le quantum q prend la valeur suivante :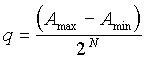 
En supposant le quantum relativement faible par rapport à la dynamique (plage de valeurs) du signal, on peut approximer le bruit de quantification (Pe) par la formule suivante :
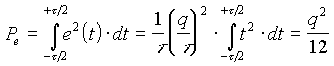
La répartition spectrale de ce bruit est uniforme dans la bande spectrale 
; cette puissance doit être comparée à celle maximale (exploitation de toute la dynamique) du signal (Pmax) pour exprimer le rapport signal à bruit (S/B) engendré par la quantification :
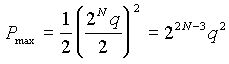
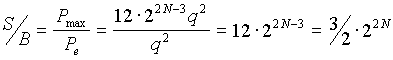
Soit, exprimé en décibels :