Menu
Général
URL: Aller
sur le site
| divergence en OU :
si 1 active et si a seul, alors désactivation de 1 et activation de 2, 3 inchangé. si a et b puis 1 active alors désactivation 1, activation 2 et 3 quel que soit leur état précédent. (règle 4) |
Convergence en OU :
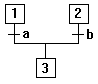
Si 1 active et a sans b, alors activation de 3 et désactivation de 1, 2 reste inchangé Si 1 et 2 et a et b alors 3 seule active |
| Divergence en ET :
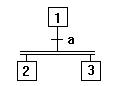
si 1 active et si a, alors désactivation de 1 et activation de 2 et 3. |
Convergence en ET :
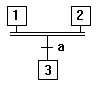
Si 1 active seule et a alors aucun changement. Si 1 et 2 et a, alors activation de 3 et désactivation de 1 et 2. |
Détaillons également le saut avant (si a alors ...)
et les boucles (répéter ... jusqu'à c). Ce sont les
deux seules possibilités avec des OU: il ne peut y avoir de divergence
en ou après une transition
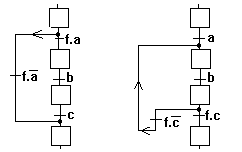
Passons maintenant à quelques problèmes plus complexes (tirés de "Comprendre et maîtriser le Grafcet, Blanchard, ed. Capadues"):
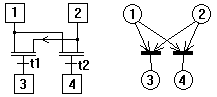
1- soient 4 étapes 1 à 4 et deux transitions de
réceptivité t1 et t2. Construire la portion de Grafcet réalisant
: Quand 1 ET 2 actifs alors
si t1 passer en 3 (et désactiver 1 et 2),
si t2 passer en 4 (et désactiver 1 et 2),
sinon rester en 1 et 2
La solution ci-dessous est accompagnée d'une représentation
de type "réseau de Petri" pour bien montrer où doivent se
placer les convergences et divergences (à quoi doit être reliée
1?, à quoi doit être reliée t1? ...). En fait on trouve
la solution facilement en analysant les cas d'évolution (quand franchit
t'on t1 ?). Il faut souligner que l'ajout d'une étape intermédiaire
n'est pas une bonne solution car tout passage d'une étape dure un
laps de temps (donc discontinuité sur les sorties = aléa
technologique)..
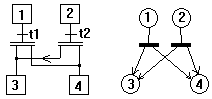
2 - Problème du même ordre : Quand (étape 1 et t1)
OU (étape 2 et t2) alors passer en 3 ET 4:
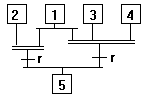
3 - si {étape 1 et [étape 2 ou (étapes 3 et 4)]}
et transition t alors activer l'étape 5 (et désactiver les
autres).
Menu
Général
URL: Aller
sur le site
