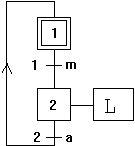
- entrées :
m : entrée E00, variable interne V00
a : entrée E01, variable interne V01
- sortie L : S20
- étapes : 1=V21, 2=V22
- transitions : 1=V11, 2=V12
Cette méthode marche sur tout automate, pour tout Grafcet. Nous l'appliquerons au cas particulier de l'AF mais le principe est rigoureusement le même sur n'importe quel langage d'automate (y compris les langages graphiques comme le langage contacts du TSX), ainsi qu'en langage machine ou même langage évolué tel Pascal ou C
On utilise une variable binaire pour représenter l'état d'activation de chaque étape, et une variable pour le franchissement de chaque transition. De plus on fige les entrées pour une durée du cycle. Il est capital de bien préciser, sur une feuille de papier, à quoi correspond chaque entrée, sortie et variable interne.
- initialisation (mise à 1 étape(s) initiale(s), à
0 les autres, mise à 0 des sorties,...)
+->- lecture des entrées (et copie dans des variables internes)
| - calcul des conditions d'évolution (quelles transitions seront franchies)
| - désactivation des étapes à désactiver
| - activation des étapes
| - combinatoire (si nécessaire: tempos, comptage, actions conditionnelles...)
| - affectation des sorties (en fonction des étapes actives)
+-------+ (saut après l'initialisation)
Remarque sur la phase de lecture des entrées : celle-ci est inutile sur
la plupart des automates simples (ils bloquent les entrées le temps d'un
cyle, ce qui les empêche des programmes du genre : boucler tant que
capteur laché). C'est la seule solution pour respecter l'algèbre
de Boole : a.(b+c) doit être équivalent à a.b + a.c
même si a change au milieu de calcul.L'ordre des phases est capital pour respecter les règles du Grafcet (surtout 4 et 5), il ne peut être modifié que dans les cas simples (en particulier quand on n'a pas besoin des règles 4 et 5).
Appliquons la méthode au Grafcet le plus simple possible, dans le seul but de bien la comprendre. Que l'on soit bien d'accord, ce problème peut se résoudre bien plus simplement (à l'aide d'un interrupteur par exemple).
|
choix
des adresses et variables internes :
- entrées : |
Début :
V21<=1 initalisation : étape 1 active
V22<=0 étape 2 non active
Boucle :
V00<=E00 lecture des entrées : copie de l'état du capteur m dans V00
V01<=E01 copie de l'état du capteur a dans B01
V11<=V00 ET V21 conditions d'évolution : transition 1 passante si étape 1 active et capteur m
V12<=V01 ET V22 transition 2 passante si étape 2 active et capteur a
SI V11 ALORS V21<=0 désactivation :si transition 1 passante, désactiver l'étape 1
Si V12 ALORS V22<=0 si transition 2 passante, désactiver l'étape 2
SI V11 ALORS V22<=1 activation : si transition 1 passante, activer l'étape 2
SI V12 ALORS V21<=1 si transition 2 passante, activer l'étape 1
S20<=V22 affectation des sorties : allumer L si étape 2 active (éteindre sinon)
SAUT Boucle boucler (mais ne pas réinitialiser)
Quelques remarques : cette méthode marche quel que soit le nombre
d'étapes actives simultanément. Le fait de bloquer les capteurs
pour un cycle allonge le temps de réaction mais donne un résultat
conforme au grafcet (si par exemple le capteur change entre le passage sur la
désactivation et l'activation). La désactivation de TOUTES les
étapes doit précéder l'activation : essayez 2
étapes qui se suivent, toutes les 2 actives, suivies de la même
réceptivité (front montant sur un capteur par exemple). Le
programme obtenu est long et lent, mais conçu rapidement (pas ou peu de
réflexion).
Mettons en oeuvre cette méthode, pour ce Grafcet, en language booléen :
Choix des variables : entrées : m : 000, mémorisé dans B00; a: 001, mémorisé dans B01. Sortie L : 020, étapes : A01 et A02, transitions : A11 et A12. La phase de mémorisation des entrées (dans B00 et B01) n'est nécessaire que sur PB100, inutile sur PB15 qui bloque les entrées le temps d'un cycle.
0C30 MU A01 initalisation : étape 1 active
0C31 MZ A02 étape 2 non active
0C32 SI 000 lecture des entrées :
0C33 ET B00 copie de l'état du capteur m dans B00
0C34 SI 001
0C35 ET B01 copie de l'état du capteur a dans B01
0C36 SI A01 conditions d'évolution :
0C37 SI B00 transition 1 passante si étape 1 active et capteur m
0C38 ET A11
0C39 SI A02
0C3A SI B01 transition 2 passante si étape 2 active et capteur a
0C3B ET A12
0C3D SI A11 désactivation :
0C3E MZ A01 si transition 1 passante, désactiver l'étape 1
0C3F SI A12
0C40 MZ A02 si transition 2 passante, désactiver l'étape 2
0C41 SI A11 activation :
0C42 MU A02 si transition 1 passante, activer l'étape 2
0C43 SI A12
0C44 MU A01 si transition 2 passante, activer l'étape 1
0C45 SI A02 affectation des sorties :
0C46 OU 020 allumer L si étape 2 active (éteindre sinon)
0C47 SAUT C32 boucler (mais ne pas réinitialiser)
Toujours pour ce même cas, supposons :
;définition des adresses PortA .def 0C0h ;registre de données du port A PortB .def 0C1h ;registre de données du port B DirA .def 0C4h ;registre de direction du port A DirB .def 0C1h ;registre de direction du port B capt .def 0A0h ;pour figer les entrées (adresse choisie parmi les 64 disponibles) etap .def 0A1h ;étapes actives trans .def 0A2h ;transitions (franchissables ou non) ;définition des constantes BitM .equ 00h ;entrée m branchée sur le bit 0 BitA .equ 01h ;entrée a branchée sur le bit 1 ;initialisation LDI DirA,00h ;tout en entrée LDI DirB,01h ;seul bit 0 en sortie, les autres inutilisés ici LDI PortB,00h ;éteindre les sorties LDI etap,01h ;étape 1 active boucle : ;scrutation des entrées LD A,PortA LD capt,A ;conditions d'évolution LDI trans,00h JRR 0,etap,trans2 ;saut plus loin si étape inactive JRR BitM,capt,trans2 ;saut plus loin si capteur éteind SET 0,trans ;allume la transition (bit 0) trans2: JRR 1,etap,desact1 JRR BitA,capt,desact1 SET 1,trans ; allume bit 1 ;désactivations desact1: JRR 0,trans,desact2 ;ne rien faire si transition non franchissable RST 0,etap desact2: JRR 1,trans,act1 ;ne rien faire si non franchissable RST 1,etap ;activations act1: JRR 0,trans,act2 ;ne rien faire si transition non franchissable SET 0,etap act2: JRR 1,trans,sorties ;ne rien faire si non franchissable SET 1,etap ;affectation des sorties sorties: LDI A,00h JRR 1,etap,FinSorties ;ne pas allumer la sortie si étape non active LDI A,01h; FinSorties: LD PortB,A ;bouclage JP boucle .END
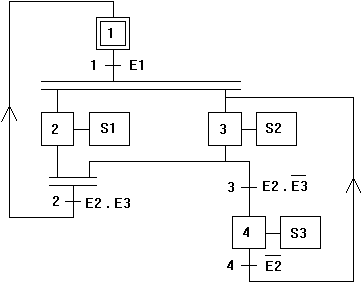
Ce grafcet a surtout un intérêt didactique : tous les ET et OU pour un minimum d'étapes.
Choix des variables (i entre 1 et 4) : étape i : ETi, transition i : TRi , entrée Ei mémorisée dans Vi
Programme correspondant en AF :
initialisation : ET1<=1 ET2<=ET3<=ET4<=0 entrees: V1<=E1 V2<=E2 V3<=E3 evolution: TR1<=ET1 ET V1 TR2<=ET2 ET ET3 ET V2 ET V3 TR3<=ET3 ET V2 ET /V3 TR4<=ET4 ET /V2 desactivation: SI (TR1) ALORS ET1<=0 SI (TR2) ALORS (ET2<=0 , ET3<=0) SI (TR3) ALORS ET3<=0 SI (TR4) ALORS ET4<=0 activation: SI (TR1) ALORS (ET2<=1 , ET3<=1) SI (TR2) ALORS ET1<=1 SI (TR3) ALORS ET4<=1 SI (TR4) ALORS ET3<=1 sorties: S1<=ET2 S2<=ET3 S3<=ET3 bouclage: SAUT entrees
Les numéros de lignes n'ont été mis que pour les premières (pour savoir où l'on doit boucler), Les suivants sont faciles à calculer. Les colonnes sont à imaginer une en dessous de l'autre.
Choix des variables : étape i : A0i, transition i : A1i, entrée Ei : 00i (et mémorisation dans B0i), sortie Si : 02i
0C30 MU A01 SI A01 SI A11 SI A11 SI A02
0C32 DE A02 SI B01 MZ A01 MU A02 OU 021
0C33 MZ A04 ET A11 SI A12 SI A11 SI A03
SI A02 MZ A03 MU A03 OU 022
0C34 SI 001 SI A03 SI A12 SI A12 SI A04
ET B01 SI B03 MZ A02 MU A01 OU 023
SI 002 SI B02 SI A13 SI A13
ET B02 ET A12 MZ A03 MU A04 SAUT C34
SI 003 SI A03 SI A14 SI A14
ET B03 SI B02 MZ A04 MU A03
SI/ B03
ET A13
SI A04 (à lire colonne après colonne)
SI/ B02
ET A14
Le pascal est le seul langage qui permette de gérer les entrées-sorties sans avoir besoin de masquages. En effet, grâce aux ensembles (SET OF), voir si un capteur est allumé se réduit à demander si le capteur appartient à l'ensemble des entrées allumées.
{ Ce programme correspond au GRAFCET 2 du poly
"mise en oeuvre du grafcet sur automate" }
PROGRAM grafcet_2 (input,output);
CONST adresse_port=$330;
TYPE liste_capteurs=(e1,e2,e3);
ensemble_capteurs=SET OF liste_capteurs;
liste_actions=(sortie1,sortie2,sortie3);
ensemble_actions=SET OF liste_actions;
VAR {pour le programme principal}
etape:array [1..4] of boolean;
transition:array [1..4] of boolean;
capteurs:ensemble_capteurs;
sorties:ensemble_actions;
i:integer;
PROCEDURE lire_capteurs(VAR etat_actuel_capteurs:ensemble_capteurs);
{cette procédure lit les capteurs et rend un ensemble contenant les
capteurs à 1. Cette procédure dépend du type de machine }
VAR {locale} etat:record case integer of
1: (compatible_port:byte);
2: (compatible_ensemble:ensemble_capteurs)
end;
BEGIN
etat.compatible_port:=port[adresse_port];
etat_actuel_capteurs:=etat.compatible_ensemble
END;
PROCEDURE affecte_sorties(etat_sorties:ensemble_actions);
{affecte les sorties}
VAR etat:record case integer of
1: (compatible_port:byte);
2: (compatible_ensemble:ensemble_actions)
end;
BEGIN
etat.compatible_ensemble:=etat_sorties;
port[adresse_port]:=etat.compatible_port
END;
BEGIN {programme principal}
{initialisation}
sorties:=[]; {ensemble vide}
affecte_sorties(sorties);
etape[1]:=true;
for i:=2 to 4 do etape[i]:=false;
REPEAT
{lecture des entrées}
lire_capteurs(capteurs);
{-----------------------------------------------
write('capteurs : ');
if e1 in capteurs then write('E1);
if e2 in capteurs then write('E2 ');
if e3 in capteurs then write('E3 ');
writeln;
------------------------------------------------}
{conditions d'évolution}
transition[1]:=etape[1] and (e1 in capteurs);
transition[2]:=etape[2] and etape[3] and ([e2,e3]*capteurs=[]); {intersection vide}
transition[3]:=etape[3] and (e2 in capteurs)
and not (e3 in capteurs);
transition[4]:=etape[4] and not (c2 in capteurs);
{désativation}
if transition[1] then etape[1]:=false;
if transition[2] then begin
etape[2]:=false;
etape[3]:=false
end;
if transition[3] then etape[3]:=false;
if transition[4] then etape[4]:=false;
{activation}
if transition[1] then begin
etape[2]:=true;
etape[3]:=true
end;
if transition[2] then etape[1]:=true;
if transition[3] then etape[4]:=true;
if transition[4] then etape[3]:=true;
{affectation sorties}
{-----------------------------------------------
write('étapes : ');
for i:=1 to 4 do if etape[i] then write(i,' ');
writeln;
------------------------------------------------}
sorties:=[];
if etape[2] then sorties:=sorties+[sortie1];
if etape[3] then sorties:=sorties+[sortie2];
if etape[4] then sorties:=sorties+[sortie3];
affecte_sorties(sorties);
UNTIL false; {boucler jusqu'à extinction}
END.
Cette méthode est beaucoup plus rapide (à l'exécution), prend beaucoup moins de place, mais ne fonctionne que pour un grafcet à une seule étape active à la fois. De plus l'automate doit pouvoir faire des sauts en avant et en arrière (ce n'est pas le cas des automates d'entrée et moyenne gamme comme le Micro 1, APRIL 15, TSX 17 à 47...).
Supposons être dans l'étape I, les sorties étant déjà affectées. On attend alors (en fonction des capteurs) que l'on doive quitter l'étape. Puis on choisit quelle doit être la suivante (au cas où l'on avait un OU divergent), on modifie les sorties si nécessaire et on saute à l'étape suivante (qui sera traitée exactement de la même manière).
On reprend le grafcet (1), avec la même affectation des entrées et des sorties.
Il ne faut plus figer les entrées, il n'est plus nécessaire de représenter les étapes par des variables puisque seule une étape est active, et elle correspond à l'endroit où l'on se trouve dans le programme.
initialisation: S20<=0; etape1: SI (/E1) SAUT etape1 ;attendre capteur m S20<=1 ;mise à jour des sorties etape2: SI (/E2) SAUT etape2 S20<=0 SAUT etape1Evidement, le programme est plus simple (mais c'est uniquement le cas dans les cas simples). Le programme est le plus rapide qui puisse exister : à un instant donné on ne teste que les capteurs nécessaires, sans aucun autre calcul. Lors d'un évolution on ne modifie que les sorties nécessaires. Le temps de réponse est donc minimal avec cette méthode. Son seul problème est qu'elle ne fonctionne qu'avec des Grafcets à une étape active à la fois (sans ET, tous les OU doivent être exclusifs) (mais voir plus bas pour résoudre ce problème)
Le PB 100 accepte les sauts généralisés, contrairement au PB15
Je ne numérote plus les lignes, mais je leur donne un nom pour que ce soit plus clair (mais il faudrait évidement mettre ces numéros avant d'entrer le programme dans l'automate).
Choix des variables : entrées : m : 000, a: 001. Sortie L : 020,
MZ 020
et1 SI/ 000 étape 1 : attendre capteur m (rester dans ces 2 lignes
SAUT et1 tant que m=0
MU 020 passage étape 1 à 2 : allumer L puis aller à étape 2
et2 SI/ 001 étape 2 : attendre capteur a
SAUT et2
MZ 020 passage 2 à 1 : éteindre L puis aller à étape 1
SAUT et1
Le grafcet (2) ne convient pas pour cette méthode, il faut d'abord le transformer en un grafcet à une seule étape active à la fois. On fait donc la table des états accessibles puis le graphe des états accessibles :.
étapes actives avant
|
transition
|
étapes
actives après
|
num
d'état
|
| 1
|
E1
|
2
3
|
(1)
|
| 2
3
|
E2.E3 E2./E1 |
1 2 4 |
(2)
|
| 2
4
|
/E2
|
2
3
|
(3)
|
on obtient donc le grafcet (3) suivant (il est rare que le graphe des états accessibles soit plus simple que l'initial) :
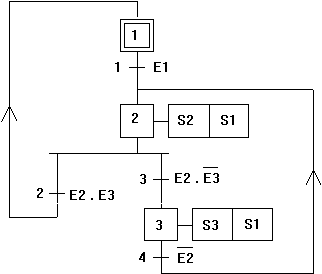
Les OU divergents DOIVENT être exclusifs (sinon vous avez oublié un cas dans la table). Si vous désirez essayer de créer un graphe des états accessibles, je vous conseille d'essayer celui là :
Vous devez arriver à un Graphe à 8 étapes (tout le monde sait faire un Grafcet à 8 étapes !). Je ne donne pas la réponse ici, ce serait trop facile (n'empêche que j'ai même réussi un jour à le faire sans intersection)
Programe en AF :
initialisation : S1<=S2<=S3<=0 etape1: SI (/E1) SAUT etape1 S2<=S1<=1 etape2: SI (/E2) SAUT etape2 ;seul E2 nécessaire pour sortir de l'étape 2 S2<=0 ;dans les 2 cas éteindre S2 SI (/E3) SAUT passage2a3 ;je traite ce cas plus loin S1<=0 ;dernière sortie à mettre à jour SAUT etape1 passage2a3: S3<=1 ;mise à jour sorties etape3: SI (E2) SAUT etape3 S3<=0 ;mise à jour sorties, inutile de modifier S1 ici S2<=1 SAUT etape2Pour la mise à jour des sorties, on sait toujours d'où l'on vient et où l'on va, on ne modifie donc que celles qui doivent l'être.
Choix des variables : entrée Ei : 00i, sortie Si : 02i
DE 021
MZ 023
et1 SI/ 001
SAUT et1
p1-2 MU 022
MU 021
et2 SI/ 002
SAUT et2
MZ 022
SI/ 003
SAUT p2-3
p2-1 MZ 021
SAUT et1
p2-3 MU 023
et3 SI 002
SAUT et3
p3-2 MZ 023
MU 022
SAUT et2
; programme en assembleur PC (sous DOS) pour le GRAFCET 3
; pour faire un .COM
code segment
assume cs:code,ds:code,es:code
org 100H
; déclarations de constantes
adresse_port_e EQU 300H ;c'est l'adresse de mon port d'entrées
adresse_port_s EQU 301H ;c'est l'adresse de mon port de sorties
c0 EQU 00000001B ;capteur E1 et sortie S1
c1 EQU 00000010B ;E2,S2
c2 EQU 00000100B ;E3,S3
; programme
; je devrais commencer par définir la direction des ports, si ma carte le permettait
s_et1: mov dx,adresse_port_s
mov al,0
out dx,al ;sorties toutes à 0
mov dx,adresse_port_e ;je laisse cette adresse par défaut dans DX
et1: in al,dx
test al,c0
jz et1
s_et2: mov dx,adresse_port_s
mov al,00000011B
out dx,al ;modif sorties
mov dx,adresse_port_e
et2: in al,dx
test al,c1
jz et2
test al,c2
jnz s_et1
s_et3: mov dx,adresse_port_s
mov al,00000101B
out dx,al
mov dx,adresse_port_e
et3: in al,dx
test al,c2
jnz et3
jmp s_et2
fin: mov ax,4C00h
int 21h
; fin du programme
code ends
end s_et1
#define port_e 0x300
#define port_s 0x301
#define e1 0x01 //sur quel bit ai-je branché l'entrée ?
#define e2 0x02
#define e3 0x04 //le suivant serait 8 puis 0x10....
#define s1 0x01 //idem sorties
#define s2 0x02
#define s3 0x04
int lecture(void)
{return(inport(port_e)); }
void ecriture(int i)
{outport(port_s, i); }
void main(void)
{
int capteurs;
etape1:
ecriture(0);
do capteurs=lecture(); while (!(capteurs&e1));
etape2:
ecriture(s1|s2);
do capteurs=lecture(); while (!(capteurs&e2);
if (capteurs&e3) goto etape1;
etape3:
ecriture(s3|s1);
co capteurs=lecture() while (capteurs&e2);
goto etape2;
}
Remarque sur le masquage : capteurs & e2 fait un ET bit à
bit entre les deux variables. Pour qu'un bit du résultat soit à
1, il faut que les bits du même niveau des DEUX variables soient à
1. Or e2 contient un seul bit à 1, celui correspondant à
l'entrée E2. Si le résultat vaut 0 (Faux), c'est que E2
était à 0, sinon (différent de 0 mais pas
nécessairement 1), c'est qu'il était alluméEn C (comme toujours) le code est compact, facile à écrire mais nécessite une conaissance plus poussée du fonctionnement de l'ordinateur (ici binaire et masquages).
Cette seconde méthode donne un programme est bien plus court dans ce cas, mais en général le graphe des états accessibles est bien plus complexe que le grafcet initial. On se débrouille en général dans ces cas complexes, de manière à minimiser la taille et le temps, en faisant un compromis entre les deux méthodes. Il n'empèche que faire par un programme la table des états accessibles est relativement aisé, et donc on peut en déduire immédiatement le programme résultant (toujours automatiquement) puisque la méthode est très simple (et correspond directement à la table)