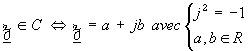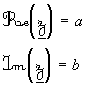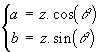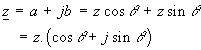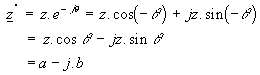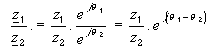| 1) Présentation.
Définition
: Le nombre imaginaire pur tel qu’élevé au carré on obtient
-1 ( on peut considérer pour l’instant que c’est pour cette raison qu’il
s’agit d’un imaginaire pur ) est noté ici « j » (contrairement à ce que
l’on trouve dans les ouvrages de mathématiques) afin qu’il n’y ait pas de
confusion possible avec l’intensité d’un courant électrique.
a) Définition cartésienne.
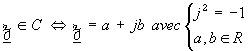 |
a est la partie réelle
b est la partie imaginaire |
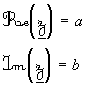 |
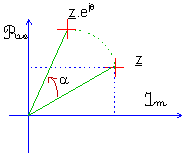
b) Représentation géométrique.
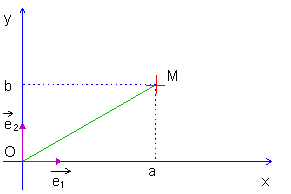
On pourra remarquer qu’il y a une
parfaite correspondance entre le plan vectoriel muni d’un repère orthonormé et le
plan complexe.
(M est appelé l’image de 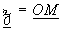 et réciproquement et réciproquement 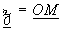 est l’affixe
de M) est l’affixe
de M)
Les deux notions sont donc parfaitement équivalentes, ce qui permet
d’employer des expressions telles que « vecteur OM ».
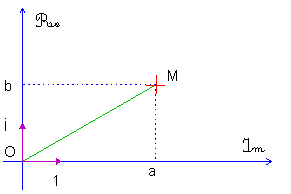
c) Module et argument.
Le module de 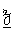 noté noté  est égal à la
norme du vecteur est égal à la
norme du vecteur 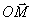 donc : donc :  L’argument de L’argument de 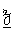 noté noté 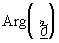 ou ou 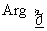 est égal à
l’angle formé entre l’axe des réels et le vecteur OM , on note est égal à
l’angle formé entre l’axe des réels et le vecteur OM , on note
 . .
Il est souvent préférable de penser à cette représentation graphique avant
d’entreprendre le moindre calcul.
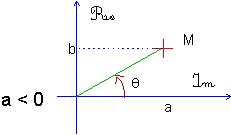
Par exemple :
si a = 0 alors l’ argument vaut π/2 ( modulo
π )
si b = 0 alors l’argument vaut 0 ( modulo π )
L’argument peut être obtenu en utilisant la fonction Arctan ( fonction
INVerse TANgente sur les calculatrices ).Cette fonction fournit un résultat compris entre
-π/2 et +π/2 , par conséquent, le résultat fourni est exact si a > 0 ,
sinon

Remarque : lorsqu'il s'agit de
faire simplement un calcul numérique, on peut utiliser la conversion
rectangulaire-polaire présente sur toutes les calculatrices scientifiques.
d) Représentation module et argument :
formule d’Euler.
Soit un nombre complexe z son module
|z| sera simplement noté z.
On peut exprimer les parties réelle a et
imaginaire b par : 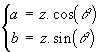 |
En réécrivant la forme cartésienne de z , on
peut écrire : 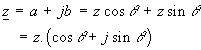 |
Le terme entre parenthèses est défini entièrement par la valeur de ce qui
permet d’exprimer z par la forme module et argument z = ( z , q ).
Cette forme n'a qu'un intérêt très limité car elle ne permet pas de faire des calculs,
on lui préfère la formule d’Euler ; on peut, dans un premier temps qu’il
s’agit d’une simple notation : 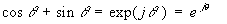
On peut donc écrire la formule d'Euler :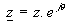 |
L’intérêt de cette formule est
qu’on peut lui appliquer les opérations valables sur les exponentielles :
la dérivation : 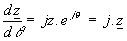 |
l’intégration : 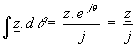 |
la multiplication et la division ( voir
ci-dessous)
2 ) Opérations sur les nombres
complexes.
a) Complexe conjugué.
C’est le (nombre) complexe ayant même
module mais l’argument opposé.
z = a + jb a pour conjugué : z* = a - jb
En effet : z = a + jb peut s’écrire : 
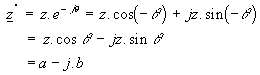 |
b) Addition et soustraction.
Soient deux nombres complexes z1
= a1 + j.b1 et z2 = a2 + j.b2
on a bien évidemment : z1 + z2 = ( a1 + a2 )
+ j.( b1 + b2 )
et z1 - z2 = ( a1 - a2 ) + j.( b1
- b2 )
c) Multiplication et division.
Soient deux nombres complexes z1
= a1 + j.b1 et z2 = a2 + j.b2
;
le produit effectué directement donne :
(a1 + j.b1 ) .(a2 + j.b2 ) = a1.a2
- b1.b2 + j.( a1.b2 + a2.b1 ) ;
on peut voir que le résultat obtenu est plus compliqué que le point de départ, il vaut
mieux ne jamais développer un produit de nombres complexes.
Il vaut mieux utiliser la formule d’Euler : 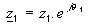 et et 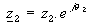 donc : donc : 
On retiendra donc que le produit de deux complexes est un complexe dont le module est
égal au produit des modules et l’argument est égal à la somme des arguments.
Module d’un produit = produit des
modules
Argument d’un produit = somme des arguments.
|
La division donne : 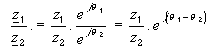
On retiendra donc que le quotient de deux complexes est un complexe dont le module
est égal au quotient des modules et l’argument est égal à la différence des
arguments.
Module d’un quotient = quotient des
modules
Argument d’un quotient = différence des arguments. |
3) Remarques.
a) Les opérateurs de rotation.
b)
Nombres complexes particuliers.
| 1 = 1 + j.0 = ( 1 , 0 ) |
-1 = -1 + j.0 = ( 1 , π ) |
| j = 0 + j.1 = ( 1 , π/2 ) |
-j = 0 +j.( - 1) = ( 1 , - π/2 ) |
|
|
| j |
est un opérateur de rotation d’angle π/2 |
| -j = 1/j |
est un opérateur de rotation d’angle - π/2 |
TETR@CORP
Copyright (c) 1998
@lterNETive. Tous droits réservés. Reproduction interdite sans autorisation.
 Webmaster d'@lterNETive Electronique Webmaster d'@lterNETive Electronique
|