Le quartz en oscillateur et en filtre
Le quartz
en oscillateur et en filtre
![]()
| Etonnant de trouver ce minéral a une tâche aussi importante en radioélectricité. Le quartz est un élément indispensable. | |
| Voyons tout d'abord
comment cela se présente dans la nature, à l'état brut. Une fois taillé convenablement, ce cristal de silice va nous être extraordinairement utile. |
|
| Et une fois travaillé par l'homme pour faire de la radio : |
|
Composition : |
|
| Le quartz est composé de silice Si O2, qui est une matière minérale extrêmement répandue dans la nature. | C'est un matériaux très dur et qui sera donc difficile à travailler, ceci expliquant en partie le prix à payer pour un quartz fait "sur mesure" |
| La
piézo-électricité : |
|
| Le quartz présente la particularité d'être piézo-électrique, en d'autres termes cela signifie que si nous lui appliquons une force de compression sur ses faces, nous constatons l'apparition de charges électriques. |
|
|
Si maintenant nous inversons l'effort que nous appliquons sur la lamelle de quartz et qu'au lieu de compresser celui-ci nous exercions une traction, nous constatons que le signe des charges s'inverse. Plus l'effort mécanique est important, plus il y a de charges qui apparaissent. |
| Mais
l'effet piézo-électrique ne s'arrête pas là, il est réversible, càd qu'en appliquant
une tension électrique sur la lamelle de quartz, on observe une déformation mécanique.
Le quartz est un matériau élastique (toutes choses égales par ailleurs) et il retrouve
sa forme originelle dès que cesse la tension. Ceci est important puisque cela dicte la fréquence propre de résonance qui est liée, entres autres, aux dimensions physiques de la lamelle de quartz. |
|
| Sur
le plan électrique : |
|
| Voici
à droite le symbole du quartz. La lamelle de quartz est reliée grâce à deux électrodes de connexion. Observez le dessin, on devine facilement que les connexions notées A et B vont constituer une magnifique capacité et cette capacité sera la capacité de connexion. |
|
| Schéma
électrique équivalent d'un quartz : |
|
|
|
Voici le schéma équivalent. On remarque immédiatement qu'il s'agit d'un circuit série shunté par une capacité, cette capacité est la capacité due aux connexions. Les valeurs de L, R et C1 sont dictées par la nature et les caractéristiques du quartz. |
| Comportement
électrique du quartz : |
|
| Appliquons
à un quartz une tension alternative sinusoïdale, faisons la varier et
mesurons l'impédance du quartz pour chaque fréquence. Nous obtenons ceci : |
|
|
|
Attention,
la courbe est beaucoup plus arrondie que cela, seule l'allure générale
est restituée par ce dessin. Hormis ceci, il n'y a pas de réelle surprise pour nous, nous reconnaissons typiquement la réaction d'un circuit série. Quand on approche de la résonance, notée Fs, l'impédance passe par un minimum équivalent sensiblement à R, puis remonte rapidement vers un maximum à la fréquence notée Fp simulant ainsi un circuit parallèle. |
| Donc tout se passe comme si nous étions en présence d'un circuit série pour une fréquence donnée et d'un circuit parallèle pour une fréquence légèrement supérieure. Ces deux fréquences Fs et Fp sont les fréquences de résonance du quartz. | |
|
|
| Son
utilité dans les oscillateurs : |
|
| Du fait de son Q très élevé et de sa stabilité, le quartz va permettre de contrôler très précisément la fréquence d'oscillation. Dès que l'on aura besoin d'une fréquence stable, on aura recours au quartz. | |
| Oscillateur
sur fréquence fondamentale : |
|
| Le
colpitts : la fréquence de résonance d'un quartz dépend de ses dimensions physiques, ceci limite forcément la fréquence maximale atteignable puisque plus la fréquence croît, plus la lamelle est mince. Pour des fréquences allant jusqu'à 30 MHz, le quartz oscille sur sa fréquence fondamentale, au dessus il faudra recourir à une astuce. A votre droite, le schéma d'un oscillateur Colpitts, la capacité en série dans le quartz permet d'ajuster (très modérément) la fréquence d'oscillation. |
|
| Le Pierce : | |
| il
existe une multitude de montages d'oscillateurs à quartz , nous ne les
passerons pas tous en revue. Si vous avez besoin de schémas d'oscillateurs à quartz, penchez-vous sur la littérature amateur qui est très riche en la matière. |
|
| Un
transistor et plusieurs quartz : |
|
|
|
Pour
votre culture personnelle et aussi par curiosité, voici un système
permettant d'utiliser un seul transistor et de commuter 3 quartz, c'est
typiquement le cas pour les oscillateurs locaux de récepteurs ou autres. Une diode est insérée en série dans chaque ensemble quartz + capacité d'accord. Quand la diode est bloquée, càd quant le potentiel +12V n'est pas appliqué à l'anode, la capacité ajustable n'est pas reliée à la masse, le circuit est ouvert. Si par l'intermédiaire du commutateur, nous appliquons le +12V sur l'anode de la diode, celle-ci conduit et le circuit retrouve la masse par la diode. La résistance en série ne fait que limiter le courant dans la diode. |
| L'oscillateur
harmonique : |
|
| Comme déjà dit, plus la fréquence demandée croît, plus la lamelle de quartz est mince, on aboutit rapidement aux limites physiques de la taille. Pour contourner ce problème, on utilise un quartz taillé pour une fréquence plus basse et on le fait osciller sur un harmonique. Pour mettre cette oscillation en évidence, l'élément actif (transistor, tube) est chargé par un circuit accordé sur | la fréquence désirée. Ce type de montage est appelé Overtone, on trouve dans le commerce des quartz pour les rangs 3,5 et 7. (harmoniques 3, 5, 7). C'est la taille particulière du quartz qui permet ceci, celui-ci est marqué sur sa fréquence finale d'oscillation, exemple 65 MHz P5. |
| Schéma
d'un tel oscillateur à FET : |
|
|
|
On note la présence dans le drain du transistor à effet de champ d'un circuit accordé composé de la self et de la capacité variable. Ce circuit permet de mettre en évidence l'harmonique de rang souhaité. On note également la présence d'un deuxième enroulement, dont une extrémité est reliée à la masse et qui est couplé au premier magnétiquement. C'est sur cet enroulement que l'on prélèvera l'énergie HF. |
| Le
VXO où comment faire varier la fréquence d'un oscillateur à quartz: |
|
|
|
|
| Nous
avons vu au début de ce chapitre qu'un quartz avait deux fréquences de
résonance propres, Fs et Fp correspondant l'une à la fréquence de
résonance série et l'autre à la fréquence de résonance parallèle. On a également vu que l'on pouvait ajuster la fréquence d'oscillation en modifiant les capacités du montage. De tout ce qui précède, l'idée de réaliser un oscillateur variable (légèrement) contrôlé par un quartz est née. |
La
grande difficulté bien sûr consiste à obtenir une variation de
fréquence suffisante pour l'application choisie et d'être certain que
cette oscillation soit bien contrôlée par le quartz. Une technique utilisée sur le génial IC202 d'ICOM dans les années 75 consiste à fabriquer un VXO sur 14 MHz puis de multiplier cette fréquence par un facteur 9. La variation de fréquence initiale est ainsi multipliée elle aussi par 9. L'iC202 couvre 200 KHz ainsi par segment sur 144 MHz |
| Le
quartz dans les filtres étroits : |
|
| Ce chapitre est censé être consacré au quartz en oscillateur. Il serait réducteur de limiter son rôle à cela car il est utilisé dans tout émetteur récepteur un tant soit peu sérieux comme filtre. | Le filtre à quartz étroit est un ensemble coûteux et indispensable ou presque. Pour les filtres à quartz les valeurs sont normalisées tant pour ce qui concerne la bande passante que la fréquence d'utilisation. |
| On trouvera essentiellement du 455 KHz (plutôt filtre céramique que quartz), du 9 MHz, du 10,7 MHz et pas mal d'autres valeurs plus ou moins exotiques. | |
| Un filtre à quartz est composé d'une suite de quartz dans le but de réduire la bande passante à la valeur souhaitée. Comme vous pouvez le constater, il n' y a rien de sorcier, rappelez-vous que ce sont seulement des équivalents à forts "Q" de circuits série mis en série |
|
| Voyons
ce que cela donne quand on fait passer un signal à travers : |
|
 |
|
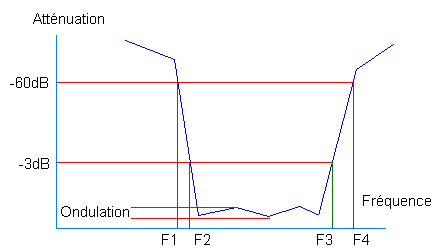
| Ci-dessus
la courbe de réponse d'un filtre à quartz, nous allons détailler ce qui
caractérise un filtre à quartz. |
|
| Fréquence centrale | Fréquence centrale de la bande passante du filtre, exemple, valeur courante en émission d'amateur 9 MHz. |
| Nombre de pôles | Nombre de quartz que contient le filtre. Typiquement 6 pôles chez les radioamateurs, parfois 8 pour les très bon filtres. |
| Perte d'insertion | Atténuation procurée par le filtre quand son atténuation est minimum. |
| Ondulation | Variation de l'atténuation dans la bande passante. Moins il y a d'ondulation, naturellement, meilleur est le filtre. |
| Bande passante à -3 dB | Voir dessin ci-dessus. La bande passante à -3 dB représente l'écart de fréquence F2-F3. |
| Bande passante à -60 dB | Voir dessin ci-dessus. La bande passante à -60 dB représente l'écart de fréquence F1-F4. |
| Facteur de forme | Cette
valeur traduit la pente du filtre. Idéalement, l'atténuation du filtre
devrait ressembler à un signal carré, ce n'est jamais le cas. On calcule
le facteur de forme comme suit : F4 - F1 FF = _________ F3 - F2 |
| Impédance de terminaison | L'impédance de charge du filtre |
| Impédance d'entrée | L'impédance d'entrée du filtre (600 W - valeur courante) |
| Phase | Différence de phase entre le signal entrant et le signal sortant |
| Délais de groupe | Concerne plus particulièrement les filtres à large bande passante, il s'agit du temps qui s'écoule pour le passage dans le filtre d'un signal modulé |
| On
ne trouve pas que des filtres à quartz pour le filtrage bande étroite, il
existe également des filtres céramiques moins onéreux mais également
moins performants. Sachez qu'un filtre à quartz 9 MHz de 2,4 kHz de bande
passante à -3 dB coûte 250 F. | |
 | |
| Ci-dessus deux filtres céramiques 455 kHz | Ci-dessus un filtre à quartz |
| Nous maîtrisons désormais le quartz et ses applications, nous pouvons passer au chapitre suivant. | |
| |