Les filtres
Les filtres
![]()
| Basés sur des éléments que nous connaissons bien, les inductances et les capacités, nous allons découvrir leur constitution et leurs caractéristiques. | ||||||||||||||
| Nécessité de
filtrer : |
||||||||||||||
| Les filtres sont indissociables de la radio, sans eux nous aurions quand même beaucoup de mal à concevoir des émetteurs et des récepteurs. | Nous avons besoin de "fenêtres" à spectre, nous avons besoin d'être sélectif, d'amplifier telle ou telle gamme de fréquence, de mettre telle ou telle autre gamme en évidence. | |||||||||||||
| Nous avons besoin de limiter notre spectre BF à la juste bande passante nécessaire à la transmission de l'information, nous avons besoin d'éliminer les harmoniques présents dans notre signal etc. | Tout cela va
être réalisé avec un assemblage savant de composants : les filtres. |
|||||||||||||
| Le filtre aura donc pour rôle de supprimer ou du moins d'atténuer fortement les signaux sur une partie du spectre, cette partie étant déterminée et par la forme et par les valeurs des constituants du filtre, et de laisser transiter avec le minimum d'atténuation possible les autres parties spectrales. | ||||||||||||||
| Typologie : |
||||||||||||||
| Avant de voir comment sont faits les filtres, nous allons étudier ce qu'ils font. | Fondamentalement il existe quarte types de filtres. | |||||||||||||
|
||||||||||||||
| Vous pouvez observer ci-dessus les courbes de réponses des quatre types de filtres. Ces courbes donnent la réponse en amplitude du filtre en fonction de la fréquence. L'axe vertical représente l'atténuation, l'axe horizontal indique la fréquence. | ||||||||||||||
| Comment
un filtre fonctionne t'il ? |
||||||||||||||
| Le principe du
filtre consiste à associer deux composants, la self et le condensateur qui ont des
comportements opposés face à une augmentation ou une diminution de fréquence en termes
de réactance.
|
||||||||||||||
| Pour un condensateur quand F croît, Z décroît | Pour une self, quand F croît, Z croît | |||||||||||||
| Un condensateur est un filtre passe haut élémentaire car sa réactance décroît quand F croît | Une self est un filtre passe bas élémentaire car sa réactance croît quand F croît | |||||||||||||
|
||||||||||||||
|
Ci-dessus sont représentées les courbes indiquant les réactances d'une self de 10 µH et d'un condensateur de 3 pF pour une fréquence évoluant de 10 à 100 MHz. |
||||||||||||||
|
Prenons le cas du filtre illustré à gauche. Quand la fréquence sera basse, la réactance de la self sera très faible tandis que la réactance du condensateur sera très élevée, le signal que l'on va appliquer à l'entrée verra une impédance quasi infinie vers la masse tandis qu'il verra une impédance très faible dans le sens du passage du filtre. | |||||||||||||
| Faisons
croître la fréquence. La réactance de la self augmente, celle du condensateur diminue.
Ceci se traduit par un passage plus difficile entre l'entrée et la sortie, une partie de
la tension est dérivée à la masse. Augmentons encore la fréquence, même principe que précédemment, peu de signal est présent en sortie. Nous avons affaire à un filtre passe bas. |
||||||||||||||
| On
pourra décrire un filtre au travers de ses caractéristiques électriques : |
||||||||||||||
| Passe bas, passe haut, passe bande, coupe bande |
|
|||||||||||||
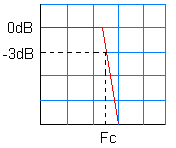 |
|
|||||||||||||
| La fréquence de coupure du filtre sera la fréquence pour laquelle l'atténuation atteint la valeur de 3dB | ||||||||||||||
| Dans la bande passante, le gain ( au mieux unitaire) peut "onduler". Cette ondulation peut prendre en fonction du filtre des valeurs de 0,5 à 1dB. Si dans la majeure partie de nos applications cela ne se révèle pas dommageable, il existe des applications ou ce critère est important |
|
|||||||||||||
|
|
|||||||||||||
| On définira l'impédance d'entrée et de sortie du filtre. |
|
|||||||||||||
| Plus le nombre de cellules est important plus la pente d'atténuation d'un filtre est importante. |
|
|||||||||||||
| Bande de fréquence dans laquelle le gain est compris entre 0 et -3dB |
|
|||||||||||||
| Remarque
: |
||||||||||||||
| Nous avons parlé
de la pente d'atténuation des filtres qui s'exprime en dB/octave ou dB/décade; un
schéma valant mieux que mille paroles, regardez ce qui suit :
|
||||||||||||||
|
||||||||||||||
|
||||||||||||||
| Composition
des filtres : |
||||||||||||||
Le filtre passe bas |
Schéma |
|||||||||||||
|
|
|||||||||||||
| On peut concevoir un filtre passe-bas de deux manières différentes comme indiqué ci-dessus, dans un cas on utilisera deux inductances et 1 condensateur, dans l'autre cas, deux condensateurs et une seule inductance. Les résultats sont identiques | ||||||||||||||
Le filtre coupe bande |
Schéma |
|||||||||||||
|
|
|||||||||||||
| En haut le circuit bouchon élémentaire, image du bas un circuit coupe bande basé sur un circuit "série" dont l'impédance est faible à la résonance et qui court-circuite à la masse les signaux. | ||||||||||||||
Le filtre passe bande |
Schéma |
|||||||||||||
|
|
|||||||||||||
| Encore une vieille connaissance, cette fois-ci il s'agit du circuit série. Son impédance est minimum à la résonance et croît rapidement en dehors de celle-ci. Seconde image, une combinaison série, // | ||||||||||||||
Le filtre passe haut |
Schéma |
|||||||||||||
|
|
|||||||||||||
| Comme pour le passe bas on peut concevoir ce type de filtre de deux façons, c.f les illustrations ci-dessus | ||||||||||||||
| Butterworth,
Bessel, Chebyshev et les autres... |
||||||||||||||
| Tous ces braves
gens (respectables mathématiciens ou physiciens) ont contribué à l'étude des filtres.
Pour un filtre passe bas, le schéma est identique, ce qui diffère c'est la valeur des
éléments, retenez bien ceci. Chaque méthode de calcul présente des avantages et des inconvénients et c'est en fonction de l'application que l'on optera pour un Butterworth ou un Chebyshev. A titre indicatif, les filtres de Butterworth présentent une impédance constante dans la bande passante, n'ondulent pas, le gain est constant, la phase des signaux est également à peu près constante. Avec un filtre de Chebyshev, l'ondulation est marquée, la phase incertaine par contre la pente d'atténuation est bcp plus raide. Regardons cela en images en observant la courbe de réponse de trois filtres passe-bas à 5 éléments ayant une fréquence de coupure Fc à - 3dB de 50 MHz |
||||||||||||||
| Filtre passe bas - réponse de Butterworth - Fc = 50 MHz | ||||||||||||||
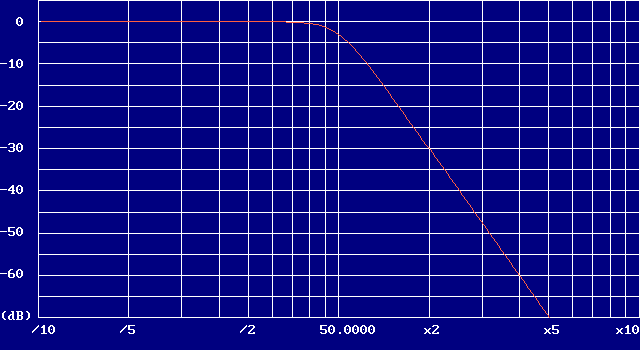 |
||||||||||||||
| Filtre passe bas - réponse de Chebyshev - Fc = 50 MHz | ||||||||||||||
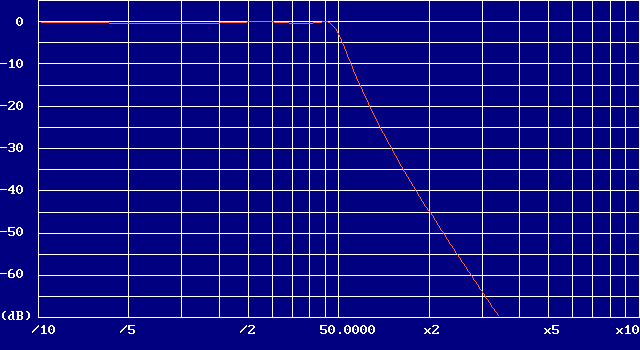 |
||||||||||||||
| Filtre passe bas - réponse de Bessel - Fc = 50 MHz | ||||||||||||||
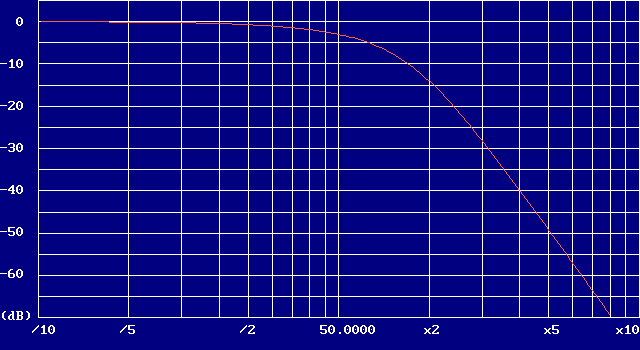 |
||||||||||||||
|
Considérations pratiques : |
||||||||||||||
| Nous venons de voir les filtres
que l'on trouve en entrée et parfois sortie de nos émetteurs récepteurs. Les selfs sont réalisées sur support torique pour d'une part diminuer les dimensions (le tore canalise le flux) par rapport aux selfs à air et d'autre part éliminer les fuites de champ magnétique. Plus la fréquence à filtrer est basse, plus les dimensions du filtre LC deviennent prohibitives, plus la pente demandée est élevée plus il faut ajouter de cellules ce qui nous ramène au problème précédent. Le calcul des filtres fait appel à des notions mathématiques complexes qui n'ont pas place ici. |
||||||||||||||
| Il existe d'autres types de filtres que les filtres LC, citons les filtres céramiques et les filtres à quartz. La finalité est la même, la mise en œuvre et la technologie sont différentes, nous aurons l'occasion d'y revenir. | ||||||||||||||
| Retour vers la page d'accueil du traité |
| Retour vers la page d'accueil du site F6CRP |
| Conception-réalisation : Denis Auquebon F6CRP |