Les filtres RC - RL

redbox.gif (41 octets)

Ce chapitre aurait dû trouver sa place avant le chapitre précédent, c'est un oubli de ma part... Nous allons étudier le fonctionnement des cellules de filtrage RC et RL, leur couplage et leurs courbes de réponse.

La cellule ou filtre RC :
Cela va vous étonner mais on peut très simplement réaliser un filtre avec un condensateur et une résistance. Il aura cette allure :

Voyons comment la bête se comporte quand elle est soumise à l'action d'une tension alternative.
La résistance se comporte comme toute résistance en présence de tension, qu'elle soit continue ou alternative, elle résiste.
La capacité, elle, présente une réactance qui est dépendante de la fréquence et de la valeur de la capacité.
 		Quand la fréquence croît, la réactance de cette capacité décroît, inversement, quand la fréquence décroît, la réactance de la capacité augmente. Ce n'est pas nouveau et vous maîtrisez bien cela.

Réalisons le montage suivant, nous nous sommes contentés de rajouter une résistance de charge notée RL.
Nous sommes donc en présence d'un simple pont diviseur formé par d'une part la résistance R et la capacité C. La charge RL est connectée au point commun.
Aux fréquences basses, la réactance du condensateur est très élevée, on peut le considérer comme un circuit ouvert, le circuit n'atténue pas, aux fréquences élevées, la réactance du condensateur est faible, on peut le considérer comme un court-circuit, le circuit atténue fortement.
Nous sommes en présence d'un filtre passe-bas.
En inversant les composants, nous obtiendrions, selon la même logique, un filtre passe haut.

A
t
t
é
n
u
a
t
i
o
n

Fréquence             


Typologie des filtres RC :
On distinguera le filtre passe-bas et le filtre passe haut, les filtres passe bande et coupe bande étant réalisé par des combinaisons des éléments précités.
Filtre passe-bas Filtre passe-haut


Fréquence de coupure des filtres RC :

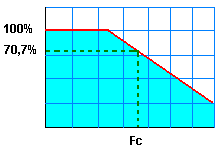
Nous trouvons, à gauche, la courbe de réponse traditionnelle d'une cellule RC passe-bas. La fréquence de coupure du filtre sera la fréquence à laquelle  l'amplitude du signal de sortie atteindra 70,7 % de l'amplitude initiale du signal.
Ceci est naturellement valable tant pour les filtres passe-bas que passe-haut.
On calculera la fréquence de coupure des ces filtres par la relation suivante :
Avec Fo en Hz
R en W
C en F



Vous pouvez légitimement vous demander d'où viennent ces 70,7%. Explications :
On détermine la fréquence de coupure des filtres à -3 dB, c'est une norme, ceci signifie que l'on mesure la fréquence du signal quand l'amplitude a chuté de 3dB (idem pour un amplificateur, sa bande passante est donnée à 3dB) et ces 3 dB correspondent au passage de 100% de signal à 70,7 %.
Donc pour déterminer quelle sera l'amplitude d'un signal connu quand ce signal chute de 3dB, il suffira d'appliquer indifféremment l'une ou l'autre des formules suivantes :


La cellule ou filtre RL :
De même que nous avons réalisé des filtres avec des résistances et des condensateurs, nous allons pouvoir fabriquer des filtres avec des résistances et des selfs suivant un principe identique.
L'inductance, comme vous le savez depuis longtemps, présente une réactance au courant alternatif. Sa loi de progression est dictée par la célèbre relation Xl = Lw avec  w = 2pf.
En clair quand la fréquence croît, la réactance croît et la self est un filtre passe-bas naturel à l'instar du condensateur qui est un filtre passe-haut naturel
Filtre passe-bas Filtre passe-haut

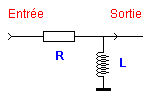
Dans le filtre ci-dessus, la réactance de la self étant faible aux basses fréquences, celles-ci seront transmises sans pratiquement d'atténuation. Au fur et à mesure que la fréquence croît, Xl croît également ce qui à pour effet d'atténuer la transmission. Ce filtre se comporte en passe-bas Inversement ici nous avons affaire à un passe-haut car aux basses fréquences, l'inductance court-circuite celles-ci vers la masse. Quand la fréquence croît, la réactance croît et son effet de court-circuit s'estompe, permettant ainsi la transmission.

Fréquence de coupure des filtres RL :
Comme pour les cellules RC, les cellules RL ont une fréquence de coupure comme cela est symbolisé sur la figure ci-contre et cette fréquence de coupure est déterminée à -3 dB.
La seule différence est que la formule de calcul de celle est différente.
Pour déterminer cela nous appliquerons pour les cellules RL passe-haut ou passe-bas la formule suivante :

Avec R en W
F en Hz
L en H
De même, comme pour les cellules RC, on pourra déterminer les tensions à - 3dB en appliquant les formules suivantes qui sont identiques pour tout type de cellule.
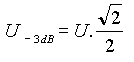ou 

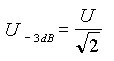
Comment retrouver les formules ?
Les formules ne sont pas le fait de la génération spontanée et il est souhaitable de pouvoir les retrouver en cas d'oubli.
 

La fréquence de coupure sera la fréquence à laquelle  la réactance (selfique ou capacitive) sera égale à la résistance
En d'autres termes, la fréquence de coupure d'un filtre RC sera atteinte quand :
Xc = R
soit   1/Cw = R    (avec w = 2pf)
soit RCw = 1  ce qui équivaut à 1= RC2pf
soit f= 1/RC2p
Le même raisonnement vaut bien sûr pour le circuit RL :
Xl = R
soit Lw = R    (avec w = 2pf)
soit L2pf = R
soit f = R/2pL
Pour en savoir plus (non indispensable pour la licence)

Comment calculer l'atténuation à une fréquence considérée ?
Nous l'avons déjà dit, le filtre RC forme un pont diviseur. Nous ferons le calcul d'atténuation à la fréquence de coupure de manière à fournir un exemple dont le résultat est connu.
Nous pouvons écrire ceci :
Il y a proportionnalité entre les tensions présentes comme l'indiquent les formules ci-contre.
La tension de sortie du filtre divisée par le tension d'entrée présente le même rapport que la réactance divisée par l'impédance du circuit.
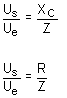Nous calculerons l'impédance d'une manière très classique et que nous connaissons bien (c'est du classique Pythagore).
Dans notre exemple, nous calculons l'atténuation à Fc ce qui veut dire, par définition que X = R, nous remplacerons systématiquement, dans les formules, X par R et ceci nous donnera :

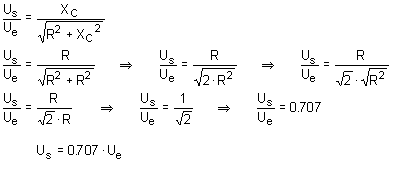Quid de l'atténuation de ce type de filtre ?
Ce type de cellule atténue de 6dB par octave, nous savons déjà ce que cela signifie car nous l'avons étudié dans le chapitre précédent.
En clair, par l'exemple, si nous avons une atténuation de 10 dB à 10 kHz pour un filtre donné, 6dB/octave équivaut à obtenir 16 dB d'atténuation à 20 kHz (on double la fréquence par octave).

Si nous souhaitions obtenir, non pas 6 dB/octave, mais 12 dB/octave, il faudrait mettre en série deux cellules.
Nous stoppons ici cette étude des cellules de filtrage RC ou RL. Elles nous permettent de bien comprendre le fonctionnement des filtres.



Retour vers la page d'accueil du traité
Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP