Le décibel

redbox.gif (41 octets)

 

Voilà une unité de mesure que vous allez employer quotidiennement. Utilisé à tout va il sert souvent d'argument définitif lors des discussions ou sur les affiches publicitaires. Il est important de bien le maîtriser.
Comme son nom l'indique, le décibel est le dixième  du Bel. On a donné ce nom à cette unité en hommage à Alexander Graham Bell. Nous voilà sacrément avancés non ? Avant d'aller plus loin sur cette merveilleuse unité qui est très simple d'emploi malgré les apparences, effectuons un petit retour en arrière et regardons in instant les logarithmes.
                 
Vous possédez sans le savoir, (peut-être) un merveilleux instrument de mesure logarithmique sur vous, je pense à votre oreille. Celle-ci ne vous restitue pas linéairement les variations de puissance auditive de votre environnement.
Si, quand vous écoutez de la musique sur votre chaîne haute fidélité, vous multipliez par 10 la puissance émise par votre amplificateur, votre sensation physiologique vous indiquera seulement un doublement de la puissance sonore.

db1.gif (1818 octets)
Vous voyez ci-dessus l'allure d'une courbe logarithmique. En clair cela signifie  que les "x" évoluent beaucoup quand parallèlement les "y" évoluent peu. Ceci pourrait être la courbe de réponse de votre oreille à une excitation sonore. sur l'axe des "x" vous trouvez l'augmentation de puissance, sur les "y" la sensation physiologique
Notation :
Vous êtes habitué à compter en base 10 (0,1,2,3,4,5,6,7,8,9) depuis votre plus tendre enfance, ceci ne vous empêche pas de savoir qu'il existe d'autres bases comme la base 2 que nous avons étudié.
Il en va de même pour les logarithmes et l'on distinguera :
Le logarithme naturel de base "e".
Il est noté log.
C'est le seul, le vrai, la référence. Si vous trouvez des résultats abracadabrants, il est à parier que votre tableur ou calculatrice ne connaît que ceux-ci alors que vous désiriez le log en base 10. Soyez attentifs à ces petites facéties.

e= 2,72
( valeur approchée)

On utilise en radioélectricité le logarithme de base 10. On passe du  logarithme naturel au logarithme en base 10 par un opération simple qui consiste à diviser  comme suit :
                     log X
Log (10) X = ________
                         log 10		 ce qui pourra s'énoncer comme suit:
le Logarithme en base 10 du nombre X sera égal au logarithme base e de X divisé par le logarithme base e de 10

Vous remarquerez que l'on note les logarithme base e avec un petit "l"(log) et les Log base 10 avec un grand "L". On trouve souvent aussi comme notation pour les base e "ln"
Exemple :


Calculons le Log base 10 de 1000 :
nous posons :

                            log 1000            6,9077
Log (10) 1000 = ________    =   __________      = 3
                                  log 10                   2,30025
Pourquoi utiliser des décibel ?
Revenons sur l'acoustique est essayons de mesurer le rapport entre le plus fort signal auditif supportable par un être humain et le plus faible. Le bruit est dû à une onde de pression. La pression la plus faible entendue par une oreille humaine se situe vers 20.10-6 Pa.
Le signal le plus fort et encore supportable avoisine les 200 000 000 10-6 Pa.
Si nous calculons le ratio du signal le plus fort sur le plus faible, nous obtenons un rapport de 10 000 000, avouez que ce n'est guère commode à manipuler. SI nous calculons le Log  de ce rapport nous trouvons R = 7 ce qui revient à dire que ce rapport est égal à 7 Bel

 
D'où vient le décibel ?
Nous venons de voir avec l'exemple précèdent  que 7 Bel représentent un rapport de 100 000 000. Le bel est une "grosse" unité, il est bien plus commode de mesurer avec une unité plus fine comme le décibel qui est le 10ème du Bel. Dans notre exemple notre rapport serait de 70 dB, c'est mieux non ?
Les décibels et la radio :
Nous avons souvent, en radioélectricité des écarts comme celui cité en exemple concernant l'oreille humaine. Prenez le plus petit signal perceptible par un récepteur et le plus fort , l'écart est encore plus important. Nous avons également besoin de quantifier les gains et les atténuations et il est plus commode de parler d'un amplificateur de 20 dB de gain que d'un amplificateur qui amplifie 100 fois. Nous avons également besoin de pouvoir ajouter ou soustraire des gains et des atténuations, avec le dB c'est ultra simple car les logarithmes ont cette merveilleuse propriété de pouvoir transformer les multiplications en additions et les divisions en soustractions. Nous avons besoin de pouvoir donner un niveau de puissance par rapport à une référence fixe, le décibel par rapport au Watt ou mW le permet. Vous l'aurez compris cette unité endémique de la radio est indispensable.
Définitions :
En puissance

Le dB est 10 fois  le logarithme base 10  du rapport de puissance P1/ P2.

                      P1
dB = 10 Log   ______
                      P2
En tension ou courant

Le dB est 20 fois  le logarithme base 10  du rapport des tensions V1/V2 uo des courants I1/I2

                     V1
dB = 20 Log   ______
                      V2
Exemple  1 :
quel est l'amplification de puissance exprimée en dB d'un amplificateur qui sort 20 W pour 1 W à l'entrée ?		                      20
A =   10 Log  ______  =   13 dB
                      1
Exemple  2 :
quel est l'atténuation de puissance exprimée en dB d'un atténuateur auquel on applique un e puissance de 100 W et qui restitue 15W		                      15
A =   10 Log  ______  =   8,2 dB
                      100
Exemple  3 :
quel est l'amplification de tension exprimée en dB d'un transistor monté en amplificateur sur lequel on mesure 3 V de tension de sortie pour 10 mV de tension d'entrée ?		                        3
A =   20 Log  ______  =   49,5 dB
                      0.01

Note : Assurez-vous quand vous faites ces calculs d'utiliser les mêmes unités. On ne peut pas calculer  avec des unités hétéroclites.

Pour votre culture personnelle, quelques propriétés des logarithmes :
  • Log ( A x B) = Log (A) + Log (B)
  • Log ( A/B) = Log (A) - Log (B)
  • si Ab = C alors  log(a) C = B   ( 102 = 100 équivaut à Log (10) 100 = 2 )
  • log Ab = B x log A

 

Application pratique des log en radioélectricité :

db2.gif (2751 octets)
Vous avez ci dessus une chaîne d'amplificateurs et d'atténuateurs. Connaissant l'atténuation ou le gain de chaque élément, il est très facile de calculer le gain/atténuation total.
  • 1er cas en dB:

    +10 - 3 +6 + 3 -20 = -4dB
    globalement cette chaîne atténue le signal appliqué en entrée

  • 2ème cas avec les rapports de puissance

    10  x 0,5 x 4 x 2 x 0,01 =  0,4
    Vérifions simplement en calculant   10 Log 0,4 = 4 dB
C'est extrêmement commode car beaucoup de données vous sont fournies en dB. Prenez l'atténuation d'un câble coaxial, on vous fournit l'atténuation en dB pour 100 m, il est aisé connaissant votre longueur d'en déduire la perte apportée.
Et l'opération inverse pour déterminer le rapport connaissant la valeur en dB ?
Connaissant la valeur en dB nous souhaitons déterminer la valeur du rapport.
A (db) sera la valeur en dB
R sera le rapport P1/P2
 Il existe au moins deux méthodes pour parvenir au résultat. Sans démonstration voici les résultats.

 db3.gif (1333 octets)

db4.gif (1282 octets)
Dans la formule ci-dessus, il est bien entendu qu'il faut utiliser le log naturel et que cette formule n'est utilisable que si le calcul a été fait en base10. Cette formule est plus simple d'emploi, toutefois la remarque concernant la base du log s'applique ici aussi
En utilisant la seconde formule et une calculatrice, calculons à quel rapport de puissance correspondent 23 dB.

R =  10 puissance 23/10    soit 10 2,3 = 200 c'est simple non ?
Tableau de quelques valeur usuelles:

en rouge, les valeurs remarquables
Rapport dB Rapport dB Rapport dB Rapport dB
1 0 20 13 100 20 1000 30
2 3 25 13.98 150 21.76 2000 33
3 4.77 30 14.77 200 23 3000 34.77
4 6 35 15.44 250 23.98 4000 36
5 6.99 40 16 300 24.77 5000 36.99
6 7.78 45 16.53 350 25.44 6000 37.78
7 8.45 50 17 400 26 7000 38.45
8 9 55 17.4 450 26.53 8000 39
9 9.54 60 17.8 500 27 9000 39.54
10 10 65 18.1 550 27.4 10000 40
11 10.4 70 18.45 600 27.78 20000 43
12 10.8 75 18.75 650 28.13 30000 44.77
13 11.14 80 19 700 28.45 40000 46
14 11.46 85 19.3 750 28.75 50000 47
15 11.76 90 19.54 800 29 100000 50

On peut souvent lire dans la littérature des phrases du genre :
La bande passante de cet ampli de puissance à -3 dB est de 4 MHz. Cela signifie que l'on note sur la courbe de puissance en fonction de la fréquence les points (supérieur et inférieur) où la puissance chute de moitié (3dB). 		L'écart entre ces deux points contitue la bande passante. Le principe est le même pour les antennes etc.
Quand vous faites ces calculs, faites attention à ne pas confondre gain en tension (sur un ampli bas niveau par exemple) et gain en puissance.
Le dBm :
Variation sur le même thème, le décibel par rapport au milliwatt.
Il est commode d'exprimer une puissance par rapport à une référence qui sera en l'occurrence le milliwatt sur une impédance de 50 W . Cette notion d'impédance de charge est importante et doit être spécifiée car 0 dBm sur 50 W  ne correspond pas à 0 dBm sur 75 W.
0 dBm sur 50 W = 224 mV sur charge de 50W = 1mW

En quoi est-ce utile ?

Nous pouvons exprimer la puissance de notre émetteur en dBm, retrancher les pertes du câble, en déduire la puissance restante, ajouter le gain de l'antenne et calculer quel sera notre signal à 800 km.
Plutôt que d'utiliser un S-mètre poussif et imprécis, il vaut mieux quantifier le signal en puissance car toute puissance correspond aussi à une tension se développant aux bornes d'une résistance. La résistance est constituée par l'antenne, votre signal chez un correspondant vaut x dBm.
Exemple : votre signal vaut -120 dBm chez un correspondant, vous multipliez votre puissance par 4 ce qui revient à ajouter 6dB (regardez le tableau ci-dessus), votre signal passera de -120 dBm à -114 dBm chez votre correspondant.
Sympa non ?
Calcul :

Vous connaissez la puissance P en milliwatt:

dBm  = 10 Log P

Vous connaissez la puissance P en watt:

dBm  = 10 Log P . 103
dBm 0 10 20 30 40 50 60 70
W 0,001 0,01 0,1 1 10 100 1000 10000
Pour passer des dBm aux milliwatt ou aux watt :
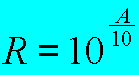db4.gif (1282 octets) Très simple ,il suffit d'appliquer cette formule .
R = puissance en milliwatt
A = dBm

Exemple : je dispose d'une puissance de 20 dBm, à quoi cela correspond t'il en mW ?
R =  10 à la puissance 20/10 , 102  = 100 mW
Le dBW:
Même principe que ci-dessus hormis que la puissance s'exprime par rapport au Watt.
On utilise cette unité pour les bilans de liaison.

Vous connaissez la puissance P en watt

dBW  = 10 Log P
Les dBi et dBd :
Ceux-ci, on les retrouve partout, plus particulièrement chez les fabricants d'antennes qui non contents de vous faire mettre de l'aluminium en l'air, aiment à entretenir une douce confusion entre ces malheureux dB.
Le dBi exprime en dB le gain d'une antenne par rapport à un aérien isotrope qui émet la même quantité d'énergie dans toutes les directions. Cet aérien n'existe pas.
le dBd exprime en dB le gain d'une antenne par rapport à un aérien dipole demi-onde. Cet aérien est une réalité physique.
Les catalogues ne spécifient pas souvent si nous avons affaire à des dB i ou d. Pourtant la différence est de taille.
Une antenne de 10dBd de gain à un gain de 12.15 dBi.
Voyez que la tentation est grande d'afficher plutôt des dBi que des dBd sans l'écrire.
Comme vous avez pu le constater, voilà une unité bien pratique et mise à toutes les sauces. Si vous ne deviez retenir qu'une chose, retenez que la valeur en dB est 10 fois le logarithme d'un rapport de puissance et 20 fois le logarithme d'un rapport de tension ou courant.



Retour vers la page d'accueil du traité
Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP