Les atténuateurs - Traité d'électricité et d'électronique pour le radioamateur

Les atténuateurs

Théorie et pratique de ces petites choses bien utiles. L'étude de l'atténuateur ouvre la porte sur des tas de nouvelles notions qui seront développées plus particulièrement lors de l'étude des antennes.

Introduction à l'atténuateur :

S'il y a une chose bien commune, que l'on retrouve dans tout le spectre de la radioélectricité, c'est bien l'atténuateur. Comme son nom le laisse entendre, l'atténuateur atténue, c'est à dire qu'il y a moins de puissance, de tension, et de courant en sortie qu'à l'entrée. Mais il ne le fait pas n'importe comment, car l'atténuateur est un ensemble d'une grande délicatesse qui préserve les caractéristiques du montage.
observons le de plus près.

Utilisations usuelles :

Réduction de puissance: Vous disposez de 10 W et votre transverter accepte maximum 1W. Un atténuateur de 10 dB fera l'affaire.
Extension de la gamme dynamique d'un appareil de mesure: Votre milliwattmètre acceptera avec plaisir 10 dB d'atténuation à l'entrée de la sonde et de fait, sa dynamique de mesure croîtra de la même valeur.
Calibration : Mesure du gain de votre préamplificateur en insérant des atténuateurs jusqu'à retrouver la valeur initiale sans préamplificateur. La valeur de l'atténuation vous donne le gain.
Adaptation d'impédance : Un atténuateur de 6dB améliore l'adaptation de 12dB. Cette astuce est souvent utilisée dans l'adaptation des mélangeurs en insérant un atténuateur 50 W.

Définition :

L'atténuateur est un dispositif souvent résistif (majoritairement) qui assume la fonction d'absorber une quantité de puissance définie tout en présentant à l'entrée comme à la sortie des impédances bien déterminées.

En d'autres termes, sa fonction est comparable à celle d'un diviseur de tension (avec pertes) qui présente la caractéristique d'avoir, par le biais de ses éléments résistifs, des impédances entrée-sortie bien maîtrisées.

On définira pour un atténuateurs les caractéristiques suivantes :

Zi impédance d'entrée en W
Z0 impédance de sortie en W
A - l'atténuation

Celle-ci pourra être exprimée en dB (ce qui est toujours le cas) et se calculera par A_dB = 10 Log A

Les deux configurations génériques :

Configuration en T

Configuration en p

Zi	Z in :Impédance d'entrée
Zo	Z out :Impédance de sortie
A	Atténuation, rapport entre sortie et entrée

Calcul des atténuateurs en T et en PI :

Vous trouverez souvent dans les formules de calcul des atténuateurs une symétrie entre les résistances R1 et R2 car les formules partent du postulat que l'impédance de sortie est égale à l'impédance d'entrée. Cette donnée, déterminée par le concepteur est vraie dans 99% des cas, toutefois dans les formules données ici vous avez la possibilité de ne pas y souscrire.

Attention : Pour le calcul, respecter rigoureusement l'ordre de calcul, pour l'atténuateur en T par exemple, commencez par calculer R3 puis R1 puis R2

Configuration en T

Configuration en p

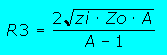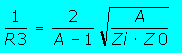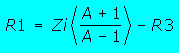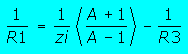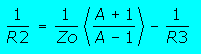Ces formules vous permettront de calculer tout type d'atténuateur ayant une impédance d'entrée différente de l'impédance de sortie. Naturellement, qui peut le plus peut le moins et elles fonctionnent pour les atténuateurs symétriques ayant Zi=Zo

Calculs d'atténuateurs symétriques :

Ayant conscience que les formules du dessus peuvent sembler rébarbatives, voici les formules simplifiées pour le cas ou Zi=Zo ce qui représente quand même l'immense majorité des cas.

Configuration en T

Configuration en p

att9.gif (1654 octets)

att10.gif (1733 octets)

Z est l'impédance caractéristique de l'atténuateur et n² est le rapport Ps/Pe, c'est à dire A dans la démonstration précédente, il faudra prendre racine de Ps/Pe pour déterminer n.

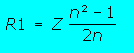C'est quand même plus simple. Attention à n et n², relisez ce qui est écrit au dessus

Et un exemple d'application :

Nous souhaitons réaliser un atténuateur de 6dB en puissance et d'impédance 50 W . Déterminons les résistances nécessaires à sa réalisation

1 - Nous savons depuis le chapitre sur le décibel que 6dB en puissance représentent un rapport de 4 donc:
n²=4 et n= 2

2 - Appliquons les formules des atténuateurs symétriques, il vient pour un atténuateur en PI

             4 - 1                     3
R1= 50 _______ =   50   _____ = 37,5 W
             2 x 2                      4

Voici le résultat, comme vous le constatez, rien de méchant.

            2 + 1                      3
R2= 50 _______ =   50   _____ = 150 W
             2 - 1                      1

Considérations pratiques concernant l'utilisation ou la fabrication d'atténuateurs :

La fabrication d'un atténuateur est chose simple mais il convient de respecter un certain nombre de règles pour obtenir un produit qui respectera les spécifications fixées. Si tel n'était pas le cas, la déception pourrait être cuisante...

En premier lieu et facteur déterminant, la qualité des résistances utilisées. Nous ne l'avons pas encore abordé mais sachez que celles-ci devront avoir un comportement en HF irréprochable, càd qu'elles devront être purement résistives sur une large plage de fréquences.

La puissance des résistances devra être compatible avec celle qu'elles devront dissiper. N'oubliez pas que l'atténuation va consister à transformer en chaleur de l'énergie HF et qu'il faudra évacuer les calories.

Le montage devra respecter la coaxialité, ce n'est pas toujours facile à réaliser. Plus simplement, nous avons pris le soin de mettre des résistances de qualité non selfiques, maintenons l'impédance fixée par un montage mécanique soigné.

Télécharger un feuille de calcul Excel pour le calcul des atténuateurs

Jouons avec les atténuateurs :

Nous allons jouer comme l'indique la tête de chapitre avec des atténuateurs mais des atténuateurs symétriques, càd que ceux-ci présentent la caractéristique Zi = Zo

Je vous propose de déterminer les caractéristiques d'un atténuateur avec un simple ohmmètre, c'est y pas génial ça ?

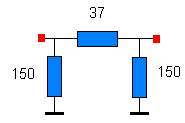Voici l'atténuateur de test, on suppose naturellement que les valeurs des résistances sont inconnues, je les ai indiquées uniquement pour pouvoir vérifier en faisant le calcul.

Déterminons l'impédance caractéristiques de l'atténuateur :

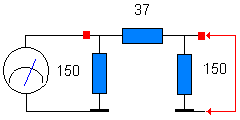
Pour ce faire, nous allons procéder à deux manipulations,

1 - Nous allons mettre un court-circuit en sortie de l'atténuateur et mesurer la résistance globale vue à l'entrée. Remarquez que nous pourrions tout aussi bien calculer cela, encore faudrait-il connaître les valeurs. L'ohmmètre indique grosso modo :
Ricc = 30 W
Ricc = résistance input sortie en cc

2 - Nous allons faire la même mesure mais cette fois-ci avec la sortie ouverte. Nous appellerons cette mesure Rio (Résistance input avec sortie ouverte)
Nous lisons :
Rio = 83,5 W

Il ne nous reste plus qu'à calculer la valeur de l'impédance caractéristique de cet atténuateur par la formule :

ce qui nous donnera :
Zc= racine ( 30x 83.5) = 50 W.
C'est commode non ? Grâce à cette manipulation simple, vous êtes en mesure désormais de déterminer l'impédance caractéristique de tout atténuateur symétrique.

Déterminons le coefficient de réflexion :

Tiens une nouveauté. Nous aurions du aborder cela dans la section antennes et lignes de transmission mais comme nous sommes en forme et bien partis...

Définition :
Le coefficient de réflexion traduit l'adaptation d'une charge à un générateur. Plus précisément il exprime la quantité de réflexion, due à la connexion générateur charge, que subit un signal.

Le coefficient de réflexion est noté :

G (Gamma) ou r (rho)
Si l'adaptation est parfaite G vaut 0, en cas de court-circuit ou de circuit ouvert G vaut -1 ou 1

Appliquons cela à notre cas, rappelons le, celui-ci représente ce qui peut se faire de pire en matière de désadaptation (ligne ouverte ou court-circuitée)

Nous avons déterminé l'impédance caractéristique de l'atténuateur à l'occasion du calcul précédent. Nous calculerons G
comme suit :

        Ricc - Zc
G =    ________
         Ricc + Zc

Les deux formules sont valides.
= coeff. de réflexion
Ricc = résist entrée sortie en CC
Rio = résist entrée sortie ouverte

        Rio - Zc
G =    ________
         Rio + Zc

Nous avons les valeurs issues des mesures précédentes, appliquons les formules :

          30 - 50              -20
G = _____________ =    _____ = - 0,25
          30 + 50                80

Déterminons le Return Loss (RL):

C'est une notion que vous verrez souvent apparaître dans la littérature amateur et professionnelle.

Le RL traduit l'adaptation entre une charge et le générateur, est exprimé en dB. On peut traduire cela par atténuation de retour.

RL = 10 Log ( G² )

Dans notre cas RL vaut : 10 Log (0,25 ²) = 12 dB

Déterminons l'atténuation de l'atténuateur :

L'atténuation vaut la moitié du RL soit AdB = RL/2
Dans notre cas AdB = 12/2 = 6dB
(cette relation n'est utilisable que dans la mesure ou la résistance de charge vaut l'impédance caractéristique).

Déterminons le ROS (tiens le voilà) :

Divers noms pour un même sujet, on retrouve ROS (Rapport d'Ondes Stationnaires), SWR (Standard Wave Ratio). On le calcul comme suit :

               1 + G
ROS =   _______
               1 - G

dans cette formule on prend
G= ( racine G²⁾

ce qui donnera pour notre exemple :

             1 + 0,251
ROS=   ____________   = 1,67
              1 - 0,251

Cet exemple permet de voir qu'avec un atténuateur de 6dB , que sa sortie soit court-circuitée ou complètement ouverte, le ROS ne pourra jamais excéder 1,67.

Nota : Il faut noter que certains calculs présentés ici ne sont valables que parce qu'on a supposé la charge identique à l'impédance caratéristique de l'atténuateur et que l'on a également considéré les charges purement résistives. La réalité est souvent fort différente et à ce moment là les calculs deviennent vraiment pénibles.

Beaucoup de nouvelles notions ont été effleurées ici, elles ne sont données qu'à titre indicatif, pour votre culture personnelle, de plus nous y reviendrons à l'occasion de l'étude des antennes et lignes de transmission.

Retour vers la page d'accueil du traité

Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP

1 + G ROS = _______ 1 - G

1 + G
ROS = _______
1 - G