Le ROS, SWR, VSWR , TOS
Le ROS, SWR, VSWR , TOS
![]()
| Le sujet qui fâche. Equivalent moderne de la lèpre moyenâgeuse pour le radioamateur, le ROS semble être la seule planche de salut à laquelle l'homo radius se raccroche, et, en fonction de la valeur affichée par la magique petite aiguille, le mental de notre bonhomme va évoluer entre l'euphorie incontrôlée et la dépression aiguë. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| La
définition : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le ROS, le SWR, le VSWR, le TOS ne font qu'exprimer, sous différentes unités, un unique et même phénomène qui est une désadaptation d'impédance (une différence) entre un élément A et un élément B. Il s'avère que ces éléments A et B sont souvent une ligne de transmission et une charge. Il n' y a rien d'autre. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| L'interprétation
qui en est faite : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quel que soit l'ouvrage consacré au sujet que vous puissiez ouvrir on va vous dire que si l'impédance de la charge diffère de l'impédance de la ligne de transmission il y aura réflexion! | La réflexion consistera en un retour depuis la charge d'une partie plus ou moins importante de l'énergie HF que vous avez envoyée vers la charge. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Et dessin à l'appui on vous montre que le courant est égal en tout point dans une ligne exempte de ROS et que dès qu'il y a ROS si vous observez le courant par exemple, vous obtenez ce que vous voyez à droite et que l'on appelle des ondes stationnaires (d'où le nom!) |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Bon tout cela est vrai, l'allure du courant ou de la tension dans la ligne est comme indiquée, par contre ce qui pèche c'est l'interprétation du phénomène et convient-il d'expliquer pourquoi cette image de la réflexion a été donnée. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Comment
se présente la charge ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Elle
peut être : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le ROS se manifestera dès lors que l'impédance de la charge sera différente de celle de la ligne de transmission. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| En
quoi le ROS est-il gênant ? |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hormis
l'aspect fixation psychologique de l'opérateur qui peut le conduire à
une névrose sévère, le ROS n'est pas l'ennemi que l'on croit. Il occasionne quelques pertes supplémentaires, encore faut-il qu'il soit élevé, il ne provoque pas d'interférences sur les TV contrairement à ce qui est dit ici ou là (au contraire il les diminue en réduisant la puissance transmise). Il peut s'avérer en revanche périlleux pour les transistors du PA qui voient une charge éloignée de celle pour laquelle ils ont été adaptés. Revenons un instant sur quelques considérations liées au courant continu. Dans les exemples ci-dessous, nous allons étudier trois cas de figure. Un générateur délivrant une tension de 100V et de résistance interne de 50 W charge une résistance qui va prendre 3 valeurs différentes, 25, 50, 75 W. Nous allons à chaque fois déterminer la puissance consommée par la charge: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
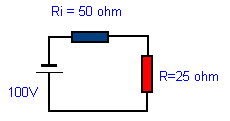 |
I=
U/R I= 100/ 50+25 = 1,33 A La puissance consommée par R : P = RI2 P = 25 x 1,332 = 44 W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
I= U/R I=
100/ 50+50 = 1 A La puissance consommée par R : P = RI2 P = 50 x 12 = 50 W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
I=
U/R I= 100/ 50+75 = 0,8 A La puissance consommée par R : P = RI2 P = 125 x 0,82 =48,6 W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Partant
de cet exemple très simple et sans démonstration, il apparaît évident
que pour obtenir un transfert optimum de puissance, il convient que la
résistance interne du générateur soit de même valeur que la
résistance de charge. Et c'est là peut-être que le ROS pourrait être le plus gênant. Nous allons essayer de quantifier tout cela ce qui nous permettra de voir qu'il faut une désadaptation sévère avant que les dégradations de signal dues au ROS soient perçues chez votre correspondant. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Appliquons
le concept de ROS au courant continu : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rappelons
ce qui est dit partout : Si une charge d'impédance Z1 est connectée à une ligne de transmission d'impédance Z2 différente, il y aura réflexion d'une partie de l'énergie en sens inverse ce qui provoquera, en fonction des phases réciproques, des ondes dites "stationnaires" dues à l'addition ou la soustraction de l'onde incidente et de l'onde réfléchie. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Essayons maintenant d'analyser ceci en continu ou l'on sait qu'un phénomène de réflexion ne peut pas se produire car le courant circule dans un sens et un seul , c'est la définition. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Adaptation parfaite | Adaptation imparfaite | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nous avons le
montage suivant : un générateur de tension continu de résistance interne 50 W alimente à travers une ligne de transmission de 50 W une charge de 50 W |
Nous avons le
montage suivant : un générateur de tension continu de résistance interne 50 W alimente à travers une ligne de transmission de 50 W une charge de 75 W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| La puissance consommée par la charge = 50W, le courant vaut 1A et la tension aux bornes de R = 50V | La puissance consommée par la charge = 48 W, le courant vaut 0,8 A et la tension aux bornes de R = 60V | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dans
le premier cas nous avons une puissance de 50W qui parvient à la charge
et qui est intégralement absorbée (transformée en chaleur). Dans le second cas, nous pourrons dire que nous avons une puissance de 50W qui arrive à la résistance de 75 W, que celle-ci absorbe 48 W et réfléchit 2W. Les 2 W réfléchis ont une amplitude de 10V qui d'une manière imaginaire peuvent s'additionner ou se soustraire dans le câble ce qui donne soit 50+ 10 = 60V soit 50-10 = 40V. Le rapport de la crête la plus élevée à la crête la plus basse 60/40 = 1,5 représente la valeur du ROS. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Il
est bien évident que c'est une vue mathématique et non physique de la
chose, cet exemple est donné ici pour illustrer le principe. Car il en
est de même en alternatif, il n' y a pas de phénomène de réflexion
physique. On devrait dire à chaque fois : "tout se passe comme si..." Ce sont les mathématiciens qui ont donné cette image facilement compréhensible mais qui ne correspond pas à la réalité physique. Nous le verrons au prochain chapitre, les ondes dites "stationnaires" sont dues au fait que quand il y a désadaptation entre ligne de transmission et charge, l'impédance vue tout au long de la ligne change continûment. Comme l'impédance n'est pas constante, le courant et la tension prennent différentes valeurs et cela se reproduit tous les 1/4 l. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quelques
définitions : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le
ROS (Rapport d'Ondes Stationnaires ou SWR ou VSWR (Voltage
Standing Wave Ratio). On peut l'exprimer de différentes manière comme nous allons le voir |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
C'est l'application mathématique de ce que nous venons de voir. Comme le ROS est toujours supérieur ou égal à 1, on utilisera la formule qui met l'impédance la plus élevée au numérateur. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Vi représente la tension incidente tandis que Vr représente la tension réfléchie. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le coefficient de réflexion : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Le coefficient de réflexion r
vaut: C'est toujours une valeur complexe, le développement de ceci ne trouve pas sa place dans cette présentation |
V réfléchie r = ____________ V incidente |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| On notera que connaissant le ROS on pourra en tirer le coeff. de réflexion |
ROS - 1 r = ____________ ROS + 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ce qui nous amène tout naturellement à déterminer le ROS partant du coefficient de réflexion par |
1 + r |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calcul
du ROS avec une charge réactive : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| C'est
quand même le cas le plus fréquent. Nous allons partir d'une hypothèse
à savoir que nous utilisons une ligne de transmission d'impédance
normalisée à 50 W
. (La formule peut prendre en compte tout type d'impédance). La charge est représentée sous forme série ( Zc = r+/- Jx ), ses valeurs sont connues. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nous allons "normaliser" à une valeur, en l'occurrence 50 W comme déjà dit en appliquant ceci | La charge à une impédance série de Zc = r +/- j x Nous normaliserons en appliquant r x R = ___ et X = ____ 50 50 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le ROS aura
pour valeur : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
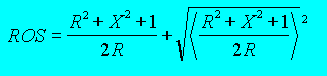 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calculateur
de ROS connaissant la puissance incidente et la puisance réfléchie |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le
TOS : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| On parlait autrefois de taux d'ondes stationnaires. Cette unité qui désigne toujours la même chose, à savoir la réflexion n'est plus guère utilisée sauf à contresens (dire qu'on a un TOS de 3 n'a pas de sens). |
Vr |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le TOS est le rapport de la tension réfléchie / la tension incidente x 100. C'est un nombre sans unité. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Calcul
du ROS à partir de la puissance directe et réfléchie. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
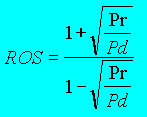
|
Si vous possédez un wattmètre
réflectomètre digne de ce nom, il vous indiquera la puisance directe et
réfléchie. Pour déterminer le ROS, appliquez la formule ci-contre. Pr = puissance réfléchie en W Pd = puissance directe en W |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Le
return loss : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| On peut exprimer d'une autre manière l'adaptation d'un système vis à vis d'un autre par une mesure appelée "return loss" ou perte de retour. | Le RL exprimé en dB représente le rapport de la puissance incidente sur la puissance réfléchie, càd la puissance non consommée par la charge du fait de la désadaptation. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Plus RL sera important meilleure sera l'adaptation, réciproquement, plus le RL sera faible plus mauvaise sera l'adaptation puisque la réflexion croît. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vous avez ci-dessus les différentes déclinaisons du return loss. A titre d'exemple imaginons que votre émetteur délivre une puissance de 100W dans un système ligne de transmission-antenne désadapté. La puissance non consommée par la charge égale 25W. Calculons le RL | RL = 10 Log
100/25 RL = 6 dB |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ci-dessus cette courbe indique le return loss en fonction du rapport des impédances. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Partant du RL, il nous sera facile (ou presque) de calculer le ROS avec la formule ci-contre. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Voici un tableau vous permettant de calculer le ROS en fonction de la puissance "réfléchie" | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Les
pertes de désadaptation : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
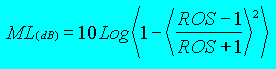 |
Elles
ont loin d'être aussi importante que ce que l'on pense
habituellement. la perte de désadaptation (ML -mismatch loss) indique de combien est atténuée la puissance incidente par la désadaptation. Cette valeur est affichée en dB, comme toujours. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Calculons pour nous amuser quelle serait la perte de désadaptation pour un système présentant un ROS de 3 soit un coefficient de réflexion de 0,5. | ML = 10 Log ( 1-
0,52) ML = 1,25 dB Avant que votre correspondant voit la différence...( en déca, en V-UHF c'est autre chose) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Et
pour finir un tableau succinct de valeurs courantes données à titre
indicatif : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Arrêtons-nous
ici car le sujet est vaste, pas forcément évident. Nous retiendrons que
le ROS provient d'une désadaptation d'impédance et que plus grande est
cette désadaptation, plus le ROS est important. Les lignes de transmission partie 2, vont compléter notre compréhension du phénomène. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Retour vers la page d'accueil du traité |
| Retour vers la page d'accueil du site F6CRP |
| Conception-réalisation : Denis Auquebon F6CRP |
|
Révision 02 du 07/02/2001 |