Les lignes  - 2ème partie

redbox.gif (41 octets)

Ceci doit vous paraître étonnant d'avoir scindé les lignes de transmission en deux parties. Ceci est dû au fait qu'il m'a semblé important de maîtriser un minimum de connaissances sur le ROS avant d'explorer plus avant les lignes de transmission.  
La longueur électrique et physique des lignes :
Il y a une différence manifeste entre la longueur physique et la longueur électrique d'une ligne qui est liée au coefficient de vélocité.
Plus le coefficient se rapproche de 1 comme pour les lignes bifilaires, plus naturellement le phénomène s'estompe.		 Il peut s'avérer utile et intéressant de connaître la longueur physique de la ligne utilisée dans la station, d'une part pour calculer les pertes et d'autre part pour tenter de calculer l'impédance qui sera vue par le transceiver si la charge à une  impédance différente de la ligne de transmission. Ce dernier est cas est plus théorique que pratique mais enfin...

                                  longueur physique
Longueur électrique= _________________
                                  coeff de vélocité

            Lp
Le =  _____
            v
Nous pouvons également exprimer la longueur de la ligne en nombre de longueur d'onde. Il suffira de diviser la longueur électrique par la longueur d'onde de la fréquence de travail

            Le
n   l  = ____
             l
Et pour terminer nous pourrons également exprimer la longueur de la ligne en degrés sachant qu'une longueur d'onde à la fréquence de travail équivaut à un tour soit 360° (n'oubliez pas que nous alimentons notre ligne en courant alternatif qui est un vecteur tournant.

            Le x 360
L° = ___________
                l
Nous allons réaliser ici une petite simulation afin de voir quelle est la longueur électrique d'une ligne de 20 m de long avec un coefficient de vélocité de 0,66 pour les différentes bandes décamétriques.

V = 0,66
L = 20m		 bandes 80m 40m 20m 15m 10m        L phy
Le = _____
           v
Longueur électrique 30,3m 30,3m 30,3m 30,3m 30,3m
Nbre l 0,35 0,7 1,41 2,12 2,83
longueur électrique
exprimée en °		 127° 254° 150° 44° 298°

 
Retour sur les pertes :
C'est un sujet que nous avons abordé. Essayons de quantifier ces pertes afin de ne plus en avoir peur.
Elles sont dues majoritairement à trois phénomènes :
  • Les pertes ohmiques car c'est aussi du courant que nous véhiculons dans des conducteurs qui bien qu'excellents ne sont pas parfaits. Plus la longueur de câble sera importante plus ce type de perte sera prononcé
  • L'effet de peau lié au précédent. Le courant alternatif ne circule pas dans l'intégralité de la section du conducteur comme c'est le cas pour le courant continu mais à sa périphérie. Plus la fréquence  croît, plus cet effet est marqué. Conséquemment, les pertes par effet de peau seront moins marquées si la superficie du conducteur est importante.
  • Les pertes diélectriques. L'isolant dans un câble coaxial n'est pas parfait et là aussi le phénomène se manifeste plus sérieusement au fur et à mesure que la fréquence croît. Il en résulte qu'une quantité d'énergie est consommée à travers lui et n'atteint donc pas la charge. On le symbolise sur le schéma équivalent d'une ligne de transmission par une résistance shunt entre les conducteurs.
  • Les pertes dues au ROS. Quand il y a du ROS dans la ligne, et le courant et la tension prennent des valeurs beaucoup plus importantes que quand le ROS = 1. Il en résulte que les pertes décrites ci-dessus augmentent ( rI2 et diélectriques)

Que faut-il en penser, essayons de quantifier les pertes :
Tout d'abord distinguons deux cas :

- en décamétrique comme nous le verrons, l'influence conjointe de ces pertes et quasiment imperceptible

- en VHF le problème n'est pas le même et il convient de "chasser le gaspi" car le niveau de bruit global est beaucoup plus faible. Reportez-vous au chapitre "le bruit" pour de plus amples explications.
Perte de signal chez son correspondant en fonction du pourcentage de puissance perdue à l'émission
Image originelle du site de W4RNL - L.B Cebik

lt22.gif (6568 octets)
Pas grand chose quand même non ?  Observez bien, avant de perte un point "S" il faut avoir perdu 75% de sa puissance d'émission et avant d'en arriver là, il faut quand même se donner du mal. Ayez toujours ce tableau présent à l'esprit.
Détruisons un mythe, observons les pertes dues au ROS sur un câble courant type RG213/KX4 avec un ROS évoluant de 1 à 5


Image originelle du site de W4RNL - L.B Cebik

lt23.gif (8691 octets)
Que pouvons nous en conclure ?

Que sur les fréquences basses, même un ROS élevé n'apporte pas une atténuation significative. Sur le haut du spectre, vers 28 MHz, passer de 1 de ROS à 5 (ce qui n'est pas rien) ne fait perdre qu'approximativement 2 dB. Vous voyez que le ROS n'est certainement pas la cause première de votre manque de réussite en DX !
Comparons maintenant les pertes dues au ROS dans une ligne bifilaire un coaxial :
Bandes : 3,5 7 10 14 18 21 24 28
coax ros=1 0,35 0,5 0,7 0,75 0,8 1 1,1 1,2
bifilaire ros=1 0,1 0,11 0,12 0,15 0,16 0,17 0,19 0,2
coax ros=5 0,75 1,2 1,4 1,7 1,9 2,1 2,2 2,5
bifilaire ros=5 0,25 0,3 0,35 0,4 0,42 0,45 0,47 0,5

On constate et on mesure la supériorité de la ligne bifilaire sur le coaxial. Rappelez-vous toutefois que la mise en oeuvre est plus délicate et demande beaucoup de soin pour arriver à ce niveau de performance.
Schéma équivalent réel d'une ligne de transmission :

lt24.gif (2353 octets)
Le seul changement perceptible consiste en la résistance shunt G qui représente les pertes diélectriques et les résistances de ligne R représentant les pertes ohmiques.
La formule permettant de calculer l'impédance de cette ligne devient :

lt25.gif (1231 octets)

Examinons ce qui se passe dans une ligne d'impédance 50 W avec une charge d'impédance différente :
Car c'est le cas de la majorité des antennes, même celles que vous prenez bien soin de tailler à la bonne longueur et que vous placez à 5m du sol. A cette hauteur (pour les bandes basses) la réaction du sol est importante et votre antenne ne présente certainement pas l'impédance théorique.
Un bon copain vous a dit qu'il suffisait de tailler le coaxial jusqu'à arriver à une valeur de ROS acceptable. Vous suivez son conseil mais vous ne parvenez pas à obtenir la valeur désirée... Que se passe t'il ?
Nous allons prendre un cas d'école. Nous avons une longueur X de câble 50 W et grâce à un appareillage idoine, nous déterminons que l'impédance de notre antenne est de 150 W. Cette antenne présente une impédance purement résistive, nous pouvons écrire :

Z = 150 +j0
Le ROS s'établit à 3 dans notre système antenne-ligne de transmission. Ce n'est pas une valeur extrême, loin s'en faut. Examinons maintenant sur une longueur d'une demi longueur d'onde puisque tous les phénomènes que nous pourrons observer se répéteront avec cette occurrence.


Image originelle du site de W4RNL - L.B Cebik

lt26.gif (11636 octets)
En vert : la réactance
en rouge : la résistance		 sur l'axe X, la longueur de la ligne observée sur 1/2 longueur d'onde et exprimée en degrés.
Analyse :
  • le ROS est constant et égal à 3.
  • la  résistance et la réactance varie continûment.
  • la réactance est capacitive de 0 à 90° puis devient inductive de 90 à 180°
  • le graphique ne le montre pas mais dès lors qu'une réactance se manifeste, un déphasage tension courant apparaît.
Ces courbes montrent que l'impédance varie continûment. Ces transformations d'impédance sont dues à la ligne de transmission qui est fermée sur une impédance différente de son impédance caractéristique. Le ROS est constant et égal à 3. Où que l'on insère le ROS-mètre, il devrait afficher la même valeur, ce qui étant donné la qualité de appareils de grande diffusion, ne sera certainement pas le cas. Ceci pourra induire en erreur l'opérateur expérimentateur qui lisant une augmentation ou une diminution (fausse) du ROS pourrait être amener à penser qu'il a réalisé une bonne adaptation ce qui n'est absolument pas le cas.
Les différences de résistances, de réactances, de phases tout au long de cette demi-onde font que le courant et la tension dans la ligne ne sont pas constants, ce sont nos fameuses ondes stationnaires. Pour vous en convaincre, notez la valeur de la résistance quand la réactance s'annule pour un angle de 20° et qui est de 15 W et de 70 W à 160°. On imagine facilement que le courant et la tension sur deux valeurs de charges différentes ne seront pas égaux.

En règle générale, on étudie graphiquement ces problèmes sur un diagramme qui porte le nom de son inventeur, l'Ingénieur Philipp Smith. Ce diagramme est toujours très utilisé, c'est vous dire son importance. Sa manipulation demande des connaissances spécifiques qui n'ont pas place ici et que d'ailleurs je serais bien incapable de donner, toutefois connaître l'allure de la bête m'a semblé important et c'est pourquoi vous voyez ceci :

lt27.gif (6923 octets)
D'une manière succincte, l'axe horizontal représente l'axe des résistances et les courbes représentent les réactances soit positives (inductives) soit négatives (capacitives) On normalise toutes les impédance à 50 W  et la valeur notée 1.0 équivaut à 50 W. Ce diagramme permet le calcul graphique d'une foultitude de données.
Calcul du ROS connaissant l'impédance caractéristique de la ligne et la résistance et la réactance de la charge :
Si nous connaissons avec certitude ces paramètres, nous pouvons aisément calculer le ROS dans la ligne de transmission. Rl= Résistance de la charge
Xl = réactance de la charge
Zo= impédance de la ligne

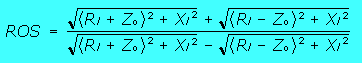lt28.gif (1872 octets)

Nous allons arrêter ici notre exploration des lignes de transmission. C'est un énorme sujet qui mérite beaucoup de développement.



Retour vers la page d'accueil du traité
Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP