Résistances en parallèle - Traité d'électricité pour le radioamateur

Le moment est venu de voir l'autre grand type d'association de résistances, l'association parallèle que nous noterons à l'avenir comme ceci "//" par souci de gain de temps (autrement nommée fainéantise)

Manipulation :

Nous avons puisé dans notre stock de composants une résistance de 10 kW et une autre de 20 kW. Nous les avons connecté comme indiqué sur le schéma à droite.
Nous nous proposons de déterminer la valeur résultante.

Cette fois-ci vous allez être surpris, car le fait de mettre en // (je l'ai fait!) deux résistances fait diminuer la résistance totale. Impossible allez-vous crier...et pourtant SI !

Comment expliquer un tel mystère ?

Mettez vous un instant à la place du courant. Vous voyez ces deux résistances devant vous (pt A), vous allez vous engouffrer dans celle qui offre le moins de résistance, ce qui déterminera un courant I1 mais il vous faudra quand même traverser celle qui offre la plus grande résistance ce qui occasionnera un courant I2 (rigolez c'est classique).
Résultat des courses : Le courant total sera égal à I1 +I2, où encore le courant total sera de toute manière plus élevé que le plus fort des courants d'une branche, ce qui démontre (on l'espère) que la valeur de 2 résistances en // est inférieure à la plus faible des deux valeurs ! Ouf. Voyons cela en termes arithmétiques.

r7.gif (2348 octets)

Approche simplifiée ne fonctionnant que pour 2 résistances en //

Rt = R1 X R2
R1 + R2

Approche académique

Pour calculer la valeur résultante d'une association de résistances R1 et R2 mise en //, nous allons passer par un calcul utilisant l'inverse de la résistance et qui s'appelle la conductance.

N'oubliez pas, pour calculer les valeurs de n résistances en //, il faut obligatoirement réduire au même dénominateur.

A titre de comparaison, si je vous donne 1/8 de tarte et 1/2 tarte, il vous est difficile de voir ce que cela représente. mentalement vous allez convertir 1/2 en x/8 ( en fait cela fait 4/8) puis vous allez ajouter 1/8 ce qui vous donnera 5/8 tarte pour vous tout seul!

1            1           1
--- =     ----- + ----     (il faut maintenant réduire
Rt         R1          R2     au même dénominateur)

1            1xR2   +    1xR1              R2 + R1
--- =      -------------------- =       ------------
Rt                 R1 x R2                R1 x R2

nous sommes en possession de 1/Rt et nous désirons
Rt donc prenons l'inverse et il vient :

Rt =        R1 X R2
               R1 + R2

Là je sens que cela flotte...un petit exemple numérique vous aiderait non ?
Supposons que nous ayons 3 résistances en // dont les valeurs sont :

R1 = 50 W
R2 = 100 W
R3 = 200 W Quelle est la résultante ? ( nous savons déjà que la valeur sera < à 50 W)

1            1       +     1    +     1
--   =    ----          ----        -----    réduisons au même dénominateur
Rt          50            100       200

1                  1 x 100 x 200       +         1 x 50 x   200          +          1 x 50 x 100
--- =           ----------------                   ------------------                   -----------------
Rt                  50 x 100 x 200                50 x 100 x 200                     50 x 100 x 200

1              20000     +   10000    +    5000                                35 000                   35
--- =        ------------------------------------       =                     ------------- =       -----
Rt                       1 000 000                                                    1 000 000             1000

Maintenant que nous savons que 1/Rt = 35/1000, inversons le rapport pour avoir Rt

Rt = 1000/35   = 28,57 W

Ceci appelle plusieurs commentaires :

1 - c'est long et fastidieux
2 - les risques d'erreurs sont nombreux
3 - La résultante est effectivement inférieure à la plus faible des valeurs en //

Bon je crois que vous avez compris, entraînez vous avec ceci :

Télécharger une feuille de calcul Excel

Testez vos connaissances

Ce n'est pas fini...Qu'en est-il de la tension et du courant dans cette association ?

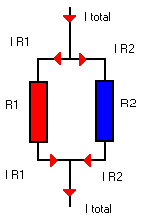Pour la tension, on voit facilement qu'elle est identique sur chaque branche, càd que la tension aux bornes de R2 = la tension aux bornes de R1. Ce sera un constante, dans une association // la tension est commune à tous les composants.

Pour le courant, le courant total se divise en deux (car 2 résistances) et sa valeur sera :

(encore la loi d'Ohm décidément universelle)

                   U                                 U
   I_R1   =   -------                I_R2 = --------
                   R1                               R2

Et pour conclure, un exemple pratique

Soit un générateur (batterie) de 60 V alimentant une association de deux résistances en //
R1 = 100
R2 = 150
Quels sont les courants qui traversent chaque résistance et quel est le courant fourni par le générateur ?

Nous pouvons soit calculer le courant dans chaque branche et sommer, soit calculer la résistance équivalente, puis le courant total, puis le courant dans chaque branche. Adoptons la solution 1
           U                  60
IR1 = ---   =         ------ =   0,6 A
           R1                100

           U                  60
IR2 = ---   =         ------ =   0,4 A
           R2                150

Le courant total = 0,6 + 0,4 = 1 A

r9.gif (2337 octets)

Et si on allait se coucher ?

A demain pour la suite...

Vérifions nos calculs

         R1 R2            100 x 150           15 000
Rt =   -------- =    ------------     = --------- = 60 W
         R1 + R2         100 + 150            250

                U                60
I total = -------   =   ------ = 1 A
                Rt               60

Voici une calculatrice javascript qui va vous permettre de réaliser quelques associations de résistances en parallèle.

Voilà, c'estfini. Ce concept des résistances // est simple, maîtrisez-le complètement.