Valeurs efficaces
Valeurs efficaces
![]()
| Nous en savons un peu plus désormais sur le courant alternatif sinusoïdal. Nous avons observé que sa valeur n'était jamais constante contrairement à celle d'un courant continu. Comment déterminer ne serait-ce que l'effet Joule avec un tel courant variable ? | |
| Observons les deux montages
suivants : |
|
 |
 |
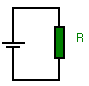
| Dans le cas ci-dessus une
résistance R est alimentée par un générateur de tension continue. Un courant I = U/R va s'établir et ce courant, par effet Joule, provoquera un échauffement de la résistance. |
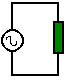
et dans le
cas ci dessus, la même résistance R est alimentée par un générateur de tension
alternative. Un courant i = u/R va s'établir et ce courant, par effet Joule, provoquera un échauffement de la résistance. |
|
|
On voit clairement qu'il sera difficile de comparer les effets de ces courants sur une même durée car ils sont très différents. Nous aurions besoin d'un coefficient nous permettant, une fois appliqué à l'un des courants d'effectuer des comparaisons. |
|
| Les physiciens ont répondu à cette épineuse question par ceci : | La puissance transformée en chaleur dans un élément résistant sera déterminée par les valeurs efficaces du signal alternatif appliqué. |
Calcul de Ieff et Ueff |
|
| Connaissant les valeurs maximales (lues sur
un oscilloscope par exemple), nous appliquerons |
|
|
|
Pour mémoire racine de 2 = 1,41 |
|
| Important: |
|
| la tension du réseau EDF de 230 V est une valeur efficace. Votre contrôleur universel affiche des valeurs efficaces, votre oscilloscope des valeurs max. | Prenez la bonne habitude de travailler avec les valeurs efficaces |
| Des
confusions à éviter: Observez bien que la tension max se mesure entre l'axe du temps et l'amplitude maximale. Vous trouverez parfois dans la littérature des tensions notée Ucàc (crête à crête) qui serviront à mesurer des puissances d'enveloppe. |
 |
| Un exemple : |
|
| On mesure sur un oscilloscope une tension crête à crête de 648 V. Quelles sont les valeurs de la tension max et efficace ? | La tension max sera égale à
la tension crête à crête divisée par 2 soit U max = Ucàc / 2 = 648/2 = 324 V Ueff = Um / (racine 2) = 324/1,41 = 230V |
| Retour vers la page d'accueil du traité |
| Retour vers la page d'accueil du site F6CRP |
| Conception-réalisation : Denis Auquebon F6CRP |