Méthode de détermination de l'impédance pour les circuits série et/ou // - Traité d'électricité pour le radioamateur

Méthode de détermination de l'impédance pour les circuits série et/ou parallèle

Si les circuits série n'offrent pas de difficultés à l'analyse, les circuits //, pour l'amateur, sont bien plus complexes à traiter.
Aussi une méthode applicable et généralisable à tous ces circuits serait la bienvenue.
C'est ce que nous allons examiner ensemble, sachant que nous sommes dans la recette de cuisine mais que cette recette fonctionne pour tous les circuits à une entrée.
Si nous avions voulu éviter l'aspect "recette", il eut fallu s'accoutumer au calcul imaginaire.

Quelques révisions (ou découvertes) :

Quand nous avons déterminé l'impédance de nos circuits série, nous avons noté cette impédance sous la forme 6,7 W , déphasage tension courant de 26,6°.

Cette notation s'appelle une notation en coordonnées polaires.
Graphiquement nous pouvons représenter ceci comme cela.

On peut aussi noter cette impédance sous forme dite "rectangulaire" et qui se décompose en deux valeurs :

1 ère partie : la valeur de la partie résistive (6 W dans l'exemple)

2 ème partie : la valeur et le signe de la réactance (+3 W dans l'exemple)

resuni1.gif (2775 octets)

Les valeurs que nous avons calculées avec nos formules d'impédance pour les circuits série nous fournissaient un résultat en coordonnées polaires, càd que Z (l'impédance du circuit) était égale à l'hypoténuse du triangle rectangle ayant pour base la résistance et pour hauteur la réactance.
Ce système est parfait mais ne nous donne pas de vision immédiate de la situation car nous ne savons pas quelle est la nature de la réactance (capacitive/inductive).
En revanche la notation en coordonnées rectangulaires nous donne immédiatement ces indications, ce qui nous fait défaut est la valeur du déphasage mais que l'on peut bien sur calculer aisément.
En résumé chaque notation qui représente les mêmes grandeurs à ses avantages et inconvénients. Vous retrouverez souvent la notation rectangulaire, autant vous y habituer.

Pour quelques détails de plus :

Voici, tiré de l'exemple ci-dessus la valeur de Z

Z = 6 + j3

Z est la valeur de l'impédance série du circuit, 6 représente la valeur résistive en ohm, et 3 la partie réactive, toujours en ohm.
et le " j " ?

Le "j" indique que nous avons affaire à une notation vectorielle et que nous ne pourrons jamais additionner 6+3. ( les vecteurs 6 et 3 sont à 90° l'un de l'autre, regardez le dessin).
Le + indique une réactance inductive, le - une réactance capacitive

Les nombres qui portent cette "marque" sont dit "nombres complexes", par extension, nous traiterons d'impédances complexes, c'est simple non ?

Les opérations sur les nombres complexes demandent quelques connaissances qui débordent plus que largement du cadre fixé, qui plus est comme déjà dit, nous allons appliquer des recettes de cuisine.

Mais, afin de peaufiner la compréhension, essayons de calculer, à partir de l'impédance complexe, la valeur polaire :
Z = 6 + j3
J'applique pythagore et hop
Z= racine ( 6² +3² )
Z= racine ( 36 + 9 ) = racine de (45) = 6,7 W.
Vous voyez, ça marche

Conventions :

Il s'agit uniquement ici de données utiles à votre culture générale, il est toutefois bon de connaître ce qui suit pour bien comprendre ce que l'on va faire dans le cadre de cette méthode

Résistance R

Z = R + j0

Inductance L

Z = 0 + jLw

Capacité C

                    1
Z = 0   - j ____
                   Cw

Ne soyez pas effrayé, c'est juste une convention d'écriture.
Vous noterez qu'il n'y a rien ici de nouveau. Si vous prenez la résistance le j0 signifie qu'il n' y a pas de réactance; pour l'inductance, sa résistance =0 et le +j devant sa réactance Lw indique que la tension est en avance sur le courant

Pour ce qui concerne la capacité, même système, il n'y a pas de résistance , c'est indiqué par le 0 et la réactance du condensateur est précédée de -j indiquant que la tension sera en retard sur courant, en d'autres termes que le courant sera en avance sur la tension.

Donc nous constatons que notre impédance est, pour tout type de composant, composée de deux parties distinctes. On les appellera :

1 - la partie réelle qui est la partie résistive de l'impédance
2 - la partie imaginaire qui est la partie réactive de l'impédance

On retiendra Z = R + jX ou Z = R - jX

Essayons appliquer nos connaissances à nos trois composants de base :

J'ai une résistance de 50 W, quelle est sa notation en impédance série ?

Là pas de question à se poser, on sait que l'impédance d'une résistance est égale à sa résistance donc Z=R donc
Z = 50 + j0

J'ai un condensateur de 100 pF, mon circuit fonctionne à la fréquence de 50 MHz, quelle sera la notation ?

Là par contre, changement car il faut tenir compte de la fréquence à laquelle est soumise le condensateur, ceci apparaît dans le terme w

1 - Calculons la réactance de C
        1                           1
X = ____    =    _____________________
       Cw          100 10^-12 x 2 x P x 50 10⁶

il vient X = 32 W, il ne reste plus qu' à écrire

Z = 0 - j32

J'ai une self de 10 µH soumise à une tension alternative de 50 MHz, quelle sera la notation ?

Même principe que pour le condensateur, nous savons que X = Lw.

1 - calculons la réactance de L

X = Lw = 10 10^-6x 2 x P x 50 10⁶= 3140 W

et Z = 0 + j 3140

Ce n'est pas difficile, ce n'est pas nouveau, vous avez déjà fait beaucoup de calculs similaires. Petite explication que nous allons utiliser dans la recette de cuisine mais qu'il n'est pas nécessaire de connaître, c'est juste pour la culture générale.
Je connais l'impédance complexe de la forme Z= 48 + j25 d'un circuit

1 - Quelle est la valeur de l'impédance du circuit ?
Facile, nous appliquons Pythagore et il vient :
Z = racine ( 48²+ 25²) = 54 W
2 - Quel est le déphasage tension courant et dans quel sens
Le sens est donné par le signe devant la réactance, ici la tension sera en avance sur le courant (circuit selfique).
Pour le déphasage nous savons que la tangente = X/R soit 25/48 = 0.52
Pour obtenir la valeur de l'angle, nous utilisons une calculette (celle de Windows convient très bien) et nous cherchons la fonction Arctangente. Toujours sur la calculette windows, il suffit de cliquer sur INV puis TAN ce qui donne : 27,5 °

3 - j'ai entendu parlé du conjugué, de quoi s'agit-il ?
Il se peut qu'à un moment, nous ayons besoin de simplifier une expression. Reprenons notre exemple où Z= 48 +j25. Le conjugué de cette expression sera 48 -J25.
Exemple :
Imaginons que nous ayons l'expression suivante :
              1
Y = __________
           48 + j25
Nous voulons simplifier et nous multiplions par le conjugué, il vient :

             48 - j25
Y =   _______________
       (48 +j25) (48 -j25)

           48- j25            48 - j25
Y = ___________ = __________
          48² + 25² 2929

Nous en savons assez pour passer à la recette !

La recette : notre objectif est d'appliquer une méthode simple nous permettant de calculer l'impédance et le déphasage d'un circuit connaissant la fréquence de travail est les éléments constitutifs du circuit.

Principe n° 1 :
Nous analyserons notre circuit en partant du premier composant, la charge, puis en rajoutant les éléments les uns après les autres en remontant vers les points de connexion. Il s'agira d'une analyse séquentielle.

Principe n° 2 :
Quand nous rajouterons un composant en parallèle, nous passerons par les admittances (vous le faites sans le savoir en continu quand vous calculez les résistances en //). Ici cela signifiera qu'avant de rajouter un composant, on calcule l'inverse de l'impédance (1/Z) qui est l'admittance Y, que l'on ajoute l'admittance du nouveau composant et que l'on calcule l'impédance par Z = 1/Y.

Principe n° 3 :
L'inverse de l'impédance est l'admittance notée Y valant 1/Z en Siemens
L'inverse de la résistance est la conductance notée G valant 1/R en Siemens
L'inverse le la réactance est la susceptance notée B valant 1/X en Siemens

Principe n° 4 :
Pour passer de Z à Y ou de Y à Z nous appliquerons systématiquement les formules suivantes sachant que toute impédance complexe sera de la forme Z= R +jX ou Z = R - jX

Partant de Z = R +jX

                 R                                X
Y = _________          - j _______
            R² + X²                     R² + X²

Partant de Y = G + jB

                 G                                B
Z = _________          - j _______
            G² + B²                     G² + B²

Résumé et synthèse de la méthode

Les équations
	Calcul de Z pour	R (1)	Z = R + j0
		C (2)	1 Z = 0 - ____ Cw
		L (3)	Z = 0 + Lw

	Passage de l'impédance à l'admittance	de Z vers Y (4)	R X Y = ______ - j _____ R² + X² R² + X²

	Passage de l'admittance vers l'impédance	de Y vers Z (5)	G B Z = ______ - j _____ G² + B² G² + B²


Démarche	1	Poser le 1er composant (la charge) Calculer son impédance Z₁= R₁ + jX₁ par formule (1-2-3)
	2	Ajouter le 2nd composant Calculer son impédance Z₂= R₂ + jX₂ par formule (1-2-3)
	3	Question :
		à placer en série ?	à placer en // ?

		Ajouter les impédances termes résistifs avec termes résistifs, termes réactifs avec termes réactifs. Z_t = Z1 + Z2 = R_t + jX_t avec Rt= R₁+R₂ et X_t = X₁ + X₂	Calculer Y1 par formule (4) Calculer Y2 par formule (4) Ajouter les admitances avec conductance avec conductance, susceptance avec susceptance Y_t= Y₁ + Y₂ = G + jB avec avec Gt= G₁+G₂ et B_t = B₁ + B₂
	4	Repasser aux impédances si nécessaire par formule (5)
	5	Ajouter composant suivant en reprenant étape 2

C'est infiniment plus simple qu'il n'y paraît. Comme toujours, nous allons mettre ceci en application avec un exemple.
Pour vous aider et éviter de fastidieux calculs (!) voici deux feuilles de calcul Excel4 à télécharger, l'une vous permet de calculer les réactances, l'autre vous permet de passer des impédances aux admittances et réciproquement.

Calcul des réactances

Calcul Z vers Y ou Y vers Z

Le problème :

Cet exemple a été tiré du livre "The ARRL UHF/Microwave experimenter's manual" que je vous engage à lire.

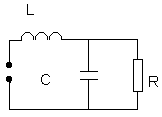
resuni2.gif (1428 octets)
L = 1µH
R = 50 W
C = 1 pF
f = 1 GHz

Nous avons le circuit ci contre à analyser. Nous désirons connaître l'impédance aux points de connexion du circuit et le déphasage s'il existe entre tension et courant.

Notre circuit fonctionne à la fréquence de 1 GHz

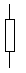1 ère étape :
positionnons le premier élément, à savoir la résistance et calculons son impédance complexe.
Ceci ne pose pas problème, c'est la définition
ZR = 50 + j0

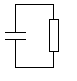resuni4.gif (1101 octets)

2 ème étape :
positionnons le deuxième élément, le condensateur en //.

Calculons la réactance ( 1/Cw ) du condensateur à 1 GHZ, il vient 159 W .
Posons la valeur de l'impédance complexe ZC = 0 - j159

Maintenant comme ces deux composants sont en //, pour déterminer la résultante, nous devons passer par les admittances.

Préalablement calculons à partir des impédances les admittances de R et C

Pour mémoire dans le cas du condensateur, (ZC= 0 -j159), 0 est la partie résistive (R) et 159 la partie réactive (X)

Pour la résistance nous savons que
Z = 50 +jo
Calculons les deux composantes de l'admittance, G et B

50
GR = __________ = 0.02 S
50² + 0²

et B=0 ( car j0)

nous écrivons :
YR= 0,02 - j0

Pour le condensateur nous savons que
Z = 0 - j159

            159
BC = _________     = 0,00629 S
            159² +0²

et G = 0 (car R=0)

nous écrirons
YC = 0 + j0,00629

nota : vous avez remarqué que le fait de passer des impédances aux admittances change le signe de la réactance.

Nous pouvons additionner les admittances ce qui donne :

Yt = YR + YC = (0,02 -j0) + (0 + j0,00629) = 0,02 + j0,00629

Nous sommes en possession de l'admittance totale de notre circuit RC

Calculons maintenant l'impédance de notre circuit, pour ce faire nous allons appliquer la formule idoine permettant de passer de Y à Z.

Pour passer de Y à Z nous appliquons :

                 G                                B
Z = _________          - j _______
            G² + B²                     G² + B²

ce qui donne :

                      0,02                                                   0,00629
Z = _________________                - j         __________________
            0,02² +0,00629²                                   0,02² +0,00629²

ceci est l'impédance du condensateur en // avec la résistance

Z = 45,5 - j14,3

3 ème étape :

Bon maintenant, nous allons connecter l'inductance en série et calculer l'impédance.

resuni2.gif (1428 octets)

Cette fois-ci l'inductance est connectée en série. Nous pourrons donc ajouter les impédances sans autre forme de procès.
Calculons l'impédance série de notre self
D'abord calculons la réactance selfique Z=Lw
Z = 1.10^-6 x 2 x p x 1.10⁹ = 6280 W
Nous allons écrire maintenant l'impédance série de notre self, il vient :
Z = 0 + j6283

Additionnons maintenant l'impédance de notre self à celle obtenue lors du calcul précédent, il vient :

Zt = Z + Zl
Zt = (45,5 - j14,3 ) + (0 +j6283) = 45,5 + j6269

ici on additionne algébriquement les résistances, donc dans cet exemple 45,5 + 0 = 45,5 et on procède de même pour les réactances comme ici -14,3 + 6283 = 6269.

Il ne nous reste plus qu'à calculer le déphasage tension courant.

Nous avons vu qu'il nous suffisait, à partir de l'impédance complexe d'appliquer X/R pour obtenir la valeur de la tangente. Nous pouvons, par la fonction arctangente, calculer directement la valeur de l'angle.
                       X                  6269
Arctangente _______ =     ________ = arctangente (137,8) = 89,6 °
                        R                  45,5

Arrêtons nous là, d'abord parce que je suis fatigué (écrire en html n'est pas aussi commode qu'il y paraît), deuxièmement parce que ces notions demandent à être digérées.
C'était peut-être un peu long et laborieux, pas très pédagogique, mais bon, après tout je ne suis pas prof, seulement accompagnateur de candidat radioamateur.

Dernier point, ceci ne fait pas partie du programme pour la licence amateur, (et fort heureusement) mais ce chapitre vous permettra, plus tard, d'appréhender bcp mieux ce qui se passe dans vos coupleurs et lignes de transmission quand vous passerez dans la catégorie "senior" (humour !)

Retour vers la page d'accueil du traité

Retour vers la page d'accueil du site F6CRP

Conception-réalisation : Denis Auquebon F6CRP