Le déphasage
Le déphasage
![]()
| Avant d'aborder les thèmes suivants consacrés aux comportements des condensateurs et inductances en alternatif, il convient de se remémorer ou de découvrir de manière simple ce que signifie le déphasage. | |
Nous allons
découvrir (très bientôt) que dans nos circuits alimentés par du courant alternatif, le
courant et la tension ne sont pas en phase. |
|
| La tension est représentée en vert, l'intensité en rouge. | Nous voyons ici que la tension démarre franchement avant le courant, peu nous importe pour le moment de savoir à quoi ceci est dû, contentons-nous de constater le phénomène. |
| Pourrions nous
représenter différemment ce déphasage ? |
|||||||||||
| oui d'une manière très simple qui consiste à utiliser un vecteur pour chaque grandeur et à les séparer de l'angle du déphasage. Regardez cet exemple |
|
||||||||||
| Nous avons un vecteur rouge d'une certaine longueur qui représente une grandeur, un vecteur bleu d'une certaine longueur qui représente une autre grandeur physique, ces vecteurs sont à 90° l'un de l'autre. | |||||||||||
| Appréhendons
sur un cycle ce que représentent les angles : et essayons de nous souvenir de la notation en radians que l'on retrouve souvent
|
|
||||||||||
|
|
|||||||||||
| Et de plus en plus
fort ... |
|||||||||||
| Imaginons que nous soyons
confrontés au problème suivant : Nous avons deux grandeurs physiques, nous savons qu'elles sont liées par un déphasage, nous ne connaissons qu'une seule de ces grandeurs. A partir de ces éléments, est-il possible de déterminer la valeur inconnue ? |
Ceci est tout à fait réalisable, nous avons seulement besoin de revoir quelques notions simple de trigonométrie. | ||||||||||
|
Vous vous
souvenez ce cet exemple que nous avions étudié ? Nous allons simplifier les choses en débarrassant ce dessin de tout ce qui encombre. |
||||||||||
| Voilà le
résultat, ne vous affolez pas, il est identique au précédent. Nous avons rajouté des
lettres désignant les côtés, à savoir : H pour l'hypoténuse O appelé côté opposé à l'angle de 60° A appelé côté adjacent à l'angle de 60 ° Vous noterez que nous avons un angle de 90° entre les segments O et A. |
|
||||||||||
Bien, que pouvons-nous faire de tout cela ? |
|||||||||||
| Résoudre un petit problème
simple par exemple. En voici les termes : Nous connaissons la longueur de H, nous connaissons la longueur de A, nous connaissons la valeur de l'angle formé par A et H, nous cherchons la longueur de O. |
La
trigonométrie nous dit : côté opposé sin (a) = __________ hypoténuse ce que nous cherchons est le côté opposé. transformons ceci comme cela et sin(a) x hypoténuse = côté opposé. |
||||||||||
| Appliquons
à un exemple numérique : Notre segment A mesure 5 m, notre segment B mesure 10m, l'angle a = 60°, quelle est la longueur de O ? |
D'après
ci-dessus Côté opposé = sin(a) x hypoténuse O= sin(60) x 10 O = 0,86 x 10 = 8,6 m |
||||||||||
| Les valeurs des sinus et
cosinus peuvent être trouvées avec un simple calculette (ou avec une règle et un compas
sur un dessin). Retenez bien que cela ne soit pas indispensable pour votre licence les relations suivantes |
|
||||||||||
côté opposé côté adjacent sin côté opposé sin (a) = __________ cos (a) = ____________ tangente = ___ = ___________ hypoténuse hypoténuse cos côté adjacent |
|||||||||||
Et Pythagore alors ? |
|||||||||||
| Nous allons voir un autre grand (très grand) théorème de géométrie qui nous sera indispensable dans les chapitres suivants, il s'agit du théorème de Pythagore | Rien n'est plus simple que le
théorème de Pythagore, n'en ayez pas peur, il va vous rendre d'immenses services, ne
serait-ce que pour tailler les haubans de votre antenne à la bonne longueur |
||||||||||
|
Regardez ceci, à gauche, c'est un triangle rectangle (ceci signifie qu'il y a un angle droit (90°) dans ce triangle) | ||||||||||
| Le théorème de Pythagore nous dit que dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. En d’autres termes, si le triangle ABC est rectangle en A, alors BC2 = AB2 + AC2 | |||||||||||
| Vous retiendrez: | |||||||||||
| car c'est ceci que nous utiliserons le plus fréquemment dans la suite de l'étude en alternatif. | 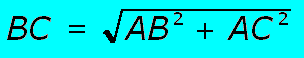 |
||||||||||
Vous demandez certainement pourquoi nous avons revu toutes ces notions et c'est bien légitime. Voici un début d'explication : Depuis longtemps vous savez que l'on ne mélange pas les serviettes et les torchons; il en va de même dans bien d'autres domaines comme nous allons le voir ici. |
|||||||||||
| Supposons que
vous habitiez La Rochelle (comme moi) et que vous ayez à vous rendre à Cahors.
Vous connaissez la distance La Rochelle Bordeaux, la distance Bordeaux Cahors mais pas la
Rochelle Cahors. Il paraît évident que si nous additionnons les distances que nous connaissons, le résultat sera supérieur à la réalité car la distance La Rochelle Cahors est bien inférieure à la distance cumulée La Rochelle Bordeaux, Bordeaux Cahors. |
|
||||||||||
| Pour
connaître la distance exacte séparant ces deux villes, nous pourrons utiliser plusieurs
méthodes toutes aussi efficaces les unes que les autres. 1 - la méthode graphique, nous dessinons à l'échelle et mesurons avec une règle 2 - la trigonométrie (sin , cos ) 3 - le théorème de Pythagore. Il en sera exactement de même pour la suite quand nous allons être confrontés à des circuits présentant des déphasages entre tension et courant. Nous ne pourrons plus ajouter simplement les grandeurs, il faudra tenir compte de l'angle de déphasage, exactement comme l'exemple routier ci-dessus. |
|||||||||||
| Voilà c'est tout pour aujourd'hui, si vous ne deviez retenir qu'une chose, retenez le théorème de Pythagore. Nous sommes désormais armés pour la suite. | |||||||||||
| Retour vers la page d'accueil du traité |
| Retour vers la page d'accueil du site F6CRP |
| Conception-réalisation : Denis Auquebon F6CRP |