Pour établir une transmission entre 2 équipements informatiques, il faut définir une liaison sur une voie de transmission munie d'éléments de transmission à ses extrémités.

L'élément de transmission peut être aussi bien un ordinateur, un terminal, ou tout autre équipement de communication.

La voie de transmission, ou canal, est une ligne téléphonique, une liaison hertzienne, ou lumineuse. Mais ce canal est régi par des caractéristiques et des contraintes auxquelles les éléments de transmission doivent s'adapter, notamment la largeur du spectre, la puissance de l'énergie transmise, les rapidités de modulation.

Pour notre projet, nous avons dû établir les caractéristiques et tenir compte des contraintes de la ligne et du système utilisé pour nous adapter.

Ce sont ces caractéristiques qui vont être définies maintenant :

Nous voulions tout d'abord suivre au mieux la base de la norme V23 (que nous n'avons d'ailleurs pas trouvée !). De cette norme, nous avons surtout gardé les fréquences des éléments binaires (0-1300Hz,1-2100Hz) et la rapidité de modulation de 1200 bauds. Partant de cela, nous respections la bande passante du Réseau Téléphonique Commuté (300-3400Hz).

Pour des raisons de simplification du système, nous avons décidé non pas de réaliser 2 modems qui puissent communiquer entre eux, mais un émetteur (Modulateur) et un récepteur (Démodulateur) avec un protocole de synchronisation qui leur est propre.

Nous allons maintenant passer en revue toutes les méthodes que nous avons utilisées pour réaliser aussi bien le modulateur que le démodulateur.

Le modulateur

La modulation FSK (Frequency Shift Keying) est un principe simple utilisé dans les transmissions bande de base et notamment dans les Modems à débit binaire faible. Une approche simple de la modulation FSK pourrait l’associer à une double modulation ASK (Tout ou Rien).

Plus simplement encore, un signal numérique binaire actionne un commutateur qui sélectionne la fréquence de l’un ou l’autre des deux oscillateurs F₁ ou F₂.
 

Au premier symbole binaire, on associe une fréquence f1                             et au second, une fréquence f2.

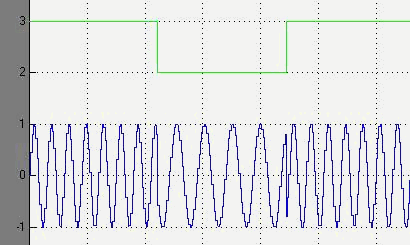
La sortie du commutateur ressemble alors au graph suivant, avec des discontinuités de phase aux instants de commutation :
 
 

L’avantage incontestable d’une telle modulation, pour la transmission bande de base, est la maîtrise de la largeur de son spectre en fonction de la bande passante du canal :
 
 
 

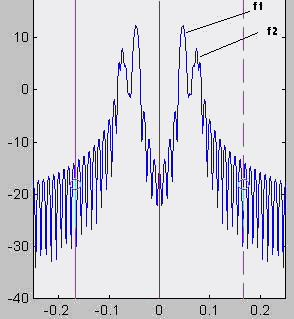Dans un canal limité, comme peut l’être une ligne du réseau téléphonique commuté (300-3400Hz), il suffit de choisir des fréquences adaptées au canal. La norme V23 du l’UIT, qui correspond à la norme qui se rapproche le plus de celle que nous avons utilisée pour notre Modem, utilise des fréquences f1=1300Hz et f2=2100Hz correspondant respectivement à la transmission d’un 0 et d’un 1. En modulation numérique, on simplifie souvent la bande passante du signal transmis à la bande de Carson égale à : BP = 2 (D f + Rb)

Mais la conception d’un modulateur est difficilement réalisable tel quel sur un système échantillonné.
En effet, il faudrait créer 2 générateurs de sinusoïdes fonctionnant en continu.

Il existe plusieurs méthodes utilisées par les systèmes à processeurs numériques pour créer une sinusoïde, et en particulier l'application d'une équation aux différences :

y[n] = 2* cos ( fn *p ) * y[n-1] - y[n-2]

avec y[-1] = sin (fn * p ) et y[-2] = 0.

Mais une méthode encore plus simple est de générer des signaux échantillonnés en faisant une lecture dans un tableau de valeurs calculé pour tracer une sinusoïde. Si on échantillonne une sinusoïde entre 0 et 2p , et que l'on place ces N valeurs d'échantillons dans une table, la modification du pas de lecture des valeurs dans le tableau modifie alors la fréquence de la sinusoïde créée.

Les valeurs du tableau correspondent à des phases uniformément distribuées entre 0 et 2p  :
                                                    y_i = 2_{i p}/ N

Pour créer les fréquences 1300Hz et 2100Hz, considérons des pas de lecture de, respectivement, 13 et 21 dans la table de Psi. La dimension de la table dépend alors exclusivement de la fréquence d’échantillonnage (Fe) du système.

Reste maintenant à calculer la taille de cette table :

Temps pour tracer une période de F₁ avec un pas de lecture de k ₁:

                                                    N = (Fe*F₁ ) / k₁

Soit, d’après nos valeurs de pas et de fréquences, N=195.

Les sinusoïdes créées par ce système ressemblent alors à :
 

En rouge, la représentation d’une fréquence de 2100 Hz, et en bleu, 1300Hz. L’échantillonnage est à peine perceptible, et les signaux une fois filtrés seront parfaitement lissés.

Une fois que le générateur de fréquence est créé, il ne reste plus qu’à transmettre les données sur la ligne sous forme de sinusoïdes à la rapidité de modulation voulue. Pour respecter dans les grandes lignes la norme V23, nous avons choisi de transmettre à environ 1200 bps. Nous verrons par la suite que, pour faire évoluer les fonctions de notre Modem, nous avons choisi de faire varier la rapidité de modulation.

Une séquence "0 1 0 1 0" FSK à 1200 bauds générée par un tel système, ressemble à:
 

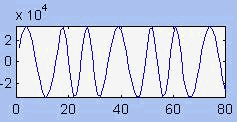La durée d'un élément binaire paraît très courte ( 1/1200 s), mais l'échantillonnage de 19532 Hz de notre modulateur permet d'obtenir environ 16 échantillons par élément binaire, avec environ 9 échantillons par période à 2100 Hz, et 15 pour une période de 1300 Hz. La condition de Shannon est respectée.

Le filtre se charge donc d'éliminer le 1^er terme correspondant à 2 fois la fréquence du signal. Il reste donc :

A²/2 cos( f (f) )

qui est une tension dont la valeur est directement fonction de f. Il ne reste plus qu'à calculer correctement la fonction du déphasage pour obtenir une différence maximale lors de la démodulation de 1300 et 2100 Hz.

En système échantillonné, le déphasage s'exprime par un retard, c'est-à-dire que l'on prend l'échantillon qui est passé k instants auparavant.

En théorie, si on reprend l'équation du signal en sortie du filtre A²/2 cos( f (f) ), f (f) s'exprime soit par (w₁ k 1/fe), soit par (w₂ k 1/fe).

La mesure du K optimum se fait donc par la fonction :

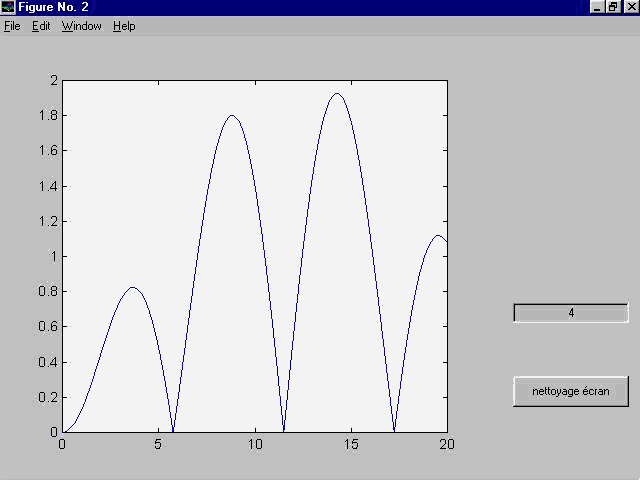Le fichier mesurek.m, accessible dans le menu Modem de l'interface graphique, permet de calculer ce retard sous MATLAB.      On remarque qu'un décalage de 9 voire de 14 apporte une différence encore plus grande, mais il faut ensuite penser au temps de calcul de l'équation dans le DSP, au nombre d'échantillons perdus par le décalage et surtout à l'erreur faite par le système lors du changement de fréquence f1 / f2. En effet, supposons un bit d’une durée de 12 échantillons et un décalage de 14, le produit se fera alors sur le bit N et sur le bit N-2, induisant une erreur sur le bit N-1.

Pour le filtre passe-bas, nous avons choisi de créer un filtre RIF (Réponse Impulsionnelle Finie) d'ordre 80, dont la fréquence de coupure se situe à la rapidité de modulation (1200 Hz).
 
 

Ce choix de fréquence de coupure du filtre s'explique simplement : Prenons le cas d’une transmission de la séquence "0 1 0 1" continue (la pire qui soit !), la forme du signal NRZ transmis est un signal carré de fréquence (rapidité de modulation) / 2 soit 600 Hz dans notre cas. Ce que nous cherchons à éliminer, c'est la composante 2*F₁ ou 2*F₂ soit au minimum 2*1300 Hz. Il faut donc choisir une fréquence de coupure entre 600 et 2300 Hz.
 
 

L'ordre du filtre que nous avons choisi correspond plus à une curiosité de notre part plutôt qu'à une nécessité, et un filtre d'ordre 60 aurait sans doute démodulé tout aussi bien. Mais lorsque l'on voit la facilité avec laquelle MATLAB et la syntaxe Algébrique de Texas Instruments gèrent les filtres, nous aurions eu bien tort de nous priver de ce petit "amusement".
 
 

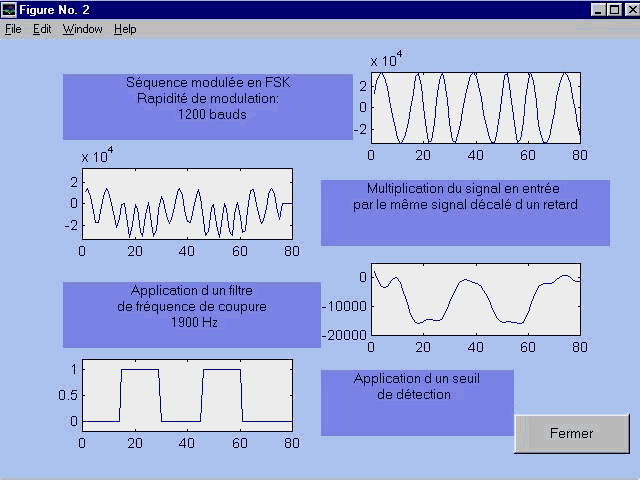
Voici donc maintenant toutes les étapes de la démodulation simulée sous MATLAB :
 
 
 
 

Comme nous venons de le voir, il n'est pas simple d'augmenter la rapidité de modulation. Celle-ci dépend tout d'abord de la fréquence d'échantillonnage.
 
 

D'après Shannon : f < 2 fe soit f < 9766 Hz
 
 

Elle est aussi limitée par la fréquence de coupure du filtre passe bas :
 
 

(Rapidité de modulation) / 2 < f coupure < 2*1300 Hz
 
 

Pour rester sûr d'obtenir une démodulation correcte, la rapidité de modulation est donc limitée à 4800 bauds.
 
 

Mais les tests et les calculs théoriques sous Matlab nous ont permis de détecter une différence du niveau du signal en sortie du filtre suivant la rapidité de modulation, nous obligeant, pour obtenir une démodulation juste, à régler le niveau du détecteur à seuil en fonction du signal.

Entre 1200 et 2400 bauds, nous avons réussi à trouver un compromis pour une démodulation correcte sans modifier le seuil du détecteur, mais pour des rapidités de modulation supérieures, il aurait fallu concevoir un système plus complexe de détection des niveaux du signal en sortie du filtre. Dans ce cas, il nous aurait été possible d'obtenir une rapidité de modulation maximale à 4800 bauds avec une fréquence de coupure aux alentours de 2500 Hz.